Difference between revisions of "Matroid"
(→References: Oxley (1992)) |
(move text from sandbox) |
||
| Line 50: | Line 50: | ||
<TR><TD valign="top">[a9]</TD> <TD valign="top">Oxley, James G. ''Matroid theory''. Oxford Science Publications. Oxford: Oxford University Press (1992). ISBN 0-19-853563-5, {{ZBL|0784.05002}}</TD></TR> | <TR><TD valign="top">[a9]</TD> <TD valign="top">Oxley, James G. ''Matroid theory''. Oxford Science Publications. Oxford: Oxford University Press (1992). ISBN 0-19-853563-5, {{ZBL|0784.05002}}</TD></TR> | ||
</table> | </table> | ||
| + | |||
| + | |||
| + | ===Greedoid=== | ||
| + | A generalisation of the concept of matroid. A greedoid on a set $V$ is a set system $\mathcal{F}$ of subset of $V$, called "feasible" sets, with the properties: 1) the empty set is feasible, $\emptyset \in \mathcal{F}$; | ||
| + | 2) if $F \in \mathcal{F}$ is non-empty, then there is $x \in F$ such that $F \setminus \{x\} \in \mathcal{F}$; 3) if $X, Y \in \mathcal{F}$ with $|X| > |Y|$ then there is $x \in X$ such that $Y \cup \{x\} \in \mathcal{F}$. | ||
| + | |||
| + | Axiom (3), the exchange property, implies that all maximal feasible sets have the same number of elements. The independent sets of a matroid form a greedoid, and the feasible sets of a greedoid form a matroid if they are hereditary, that is, axiom (2) holds in the strong form that for every $x \in F$, $F \setminus \{x\} \in \mathcal{F}$. | ||
| + | |||
| + | ====References==== | ||
| + | * Björner, Anders; Ziegler, Günter M. "Introduction to greedoids", ''Matroid applications'', ed Neil White, Encycl. Math. Appl. '''40''', Cambridge University Press (1992) 284-357. ISBN 0-521-38165-7 Zbl 0772.05026 | ||
Revision as of 15:14, 20 November 2014
A combinatorial abstraction of a linear algebra. A matroid is specified by a set 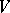 of elements and a family
of elements and a family 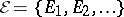 of subsets of
of subsets of 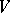 , called independent subsets, which satisfy the following axioms: 1) the empty set is independent; 2) any subset of an independent set is independent; 3) for every subset
, called independent subsets, which satisfy the following axioms: 1) the empty set is independent; 2) any subset of an independent set is independent; 3) for every subset 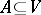 , all the independent subsets of the matroid which are contained in
, all the independent subsets of the matroid which are contained in 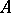 and are maximal with respect to inclusion relative to
and are maximal with respect to inclusion relative to 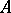 have the same number of elements.
have the same number of elements.
Examples. 1) The set 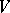 of rows of an arbitrary rectangular matrix and the family
of rows of an arbitrary rectangular matrix and the family 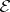 of all subsets of
of all subsets of 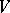 consisting of linearly independent rows form a matroid. 2) Let
consisting of linearly independent rows form a matroid. 2) Let 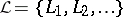 be the set of all skeleton forests (see Tree) of a graph
be the set of all skeleton forests (see Tree) of a graph 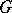 , and let
, and let 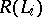 be the set of edges of the forest
be the set of edges of the forest 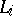 ,
, 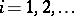 . Then the set
. Then the set 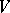 of edges of the graph
of edges of the graph 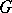 and the family
and the family 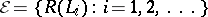 form a matroid. 3) Let
form a matroid. 3) Let 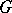 be a bipartite graph (cf. Graph, bipartite) with parts
be a bipartite graph (cf. Graph, bipartite) with parts 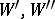 . A subset
. A subset 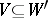 of vertices for which there is a matching
of vertices for which there is a matching 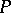 of the graph
of the graph 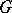 such that every vertex
such that every vertex 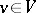 is incident to some edge of
is incident to some edge of 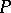 is called a partial transversal. The set
is called a partial transversal. The set 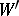 and the set of all transversals of the graph
and the set of all transversals of the graph 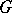 form a so-called transversal matroid.
form a so-called transversal matroid.
A matroid can be also specified by a set 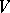 of elements and a family
of elements and a family 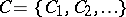 of non-empty subsets
of non-empty subsets 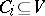 , called circuits, which satisfy the following axioms: no proper subset of a circuit is a circuit; and if
, called circuits, which satisfy the following axioms: no proper subset of a circuit is a circuit; and if 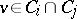 , then
, then 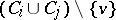 contains a circuit. The independent subsets of this matroid are the subsets
contains a circuit. The independent subsets of this matroid are the subsets 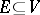 that do not contain circuits.
that do not contain circuits.
If 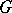 is a graph, then the set of its edges and the family of its simple circuits form what is called a graphic matroid. If for the circuits of a matroid one takes the cocycles (cuts, cf. Graph, connectivity of a) of the graph
is a graph, then the set of its edges and the family of its simple circuits form what is called a graphic matroid. If for the circuits of a matroid one takes the cocycles (cuts, cf. Graph, connectivity of a) of the graph 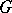 , the resulting matroid is called a cographic matroid. The matroids of the last two types are also termed cyclic and cocyclic. The notion of a "matroid" is used in graph theory and combinatorics in the proof of some assertions on covering and packing of matchings.
, the resulting matroid is called a cographic matroid. The matroids of the last two types are also termed cyclic and cocyclic. The notion of a "matroid" is used in graph theory and combinatorics in the proof of some assertions on covering and packing of matchings.
References
| [1] | H. Whitney, "On the abstract properties of linear dependence" Amer. J. Math. , 57 (1935) pp. 509–533 |
| [2] | W.T. Tutte, "Lectures on matroids" J. Res. Nat. Bur. Standards Sec. B , 69 : 1–2 (1965) pp. 1–47 |
Comments
The example of the matroid consisting of the rows of a (rectangular) matrix gave rise to the name.
In matroid theory, most often the underlying set 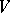 is supposed to be finite. And, in fact, it is not particularly clear what the right definitions are in the infinite case (cf. [a1], Chapt. 20). For a finite
is supposed to be finite. And, in fact, it is not particularly clear what the right definitions are in the infinite case (cf. [a1], Chapt. 20). For a finite  the third independence axiom (given the other 2) is equivalent to
the third independence axiom (given the other 2) is equivalent to 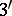 ) If
) If 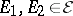 and
and 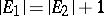 , then there is a
, then there is a 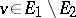 such that
such that 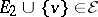 .
.
There are many axiom systems for matroids. In addition to those based on the ideas of independent subsets and circuits there are axiom systems based on the idea of a rank function, the idea of a basis, the idea of a hyperplane, or the idea of a closure operation.
A maximal independent set is called a basis (and a minimal dependent set is called a circuit or cycle of the matroid). The maximal cardinality of an independent set contained in a subset 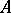 of
of 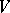 is called the rank
is called the rank 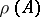 . Given
. Given 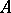 , the set
, the set 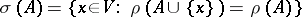 is called the closure of
is called the closure of 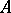 ; one calls
; one calls 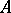 closed if and only if
closed if and only if 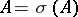 . A maximal (proper) closed subset
. A maximal (proper) closed subset 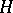 of
of 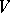 is called a hyperplane.
is called a hyperplane.
For a finite 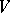 the "basis axiomatization" is as follows. A non-empty collection
the "basis axiomatization" is as follows. A non-empty collection 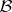 of subsets of
of subsets of 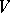 is the set of bases of a matroid if and only if for all
is the set of bases of a matroid if and only if for all 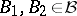 and
and 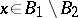 there is an
there is an 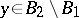 such that
such that 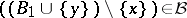 .
.
A closure operation on a set 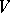 is a mapping
is a mapping 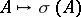 of subsets of
of subsets of 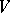 to subsets of
to subsets of 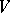 such that
such that 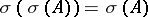 ,
, 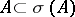 ,
, 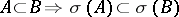 . Such a closure operation defines a matroid if for all
. Such a closure operation defines a matroid if for all 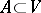 ,
, 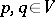 ,
, 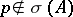 one has
one has 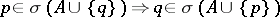 (the exchange axiom). The corresponding independent subsets are defined by:
(the exchange axiom). The corresponding independent subsets are defined by: 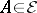 if and only if
if and only if 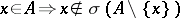 .
.
Given any matroid 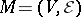 , there is a dual matroid
, there is a dual matroid 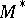 , which is most simply defined in terms of bases as follows: If
, which is most simply defined in terms of bases as follows: If 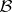 is the set of all bases of
is the set of all bases of 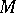 , then the set
, then the set 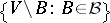 is the set of bases of
is the set of bases of 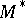 . The duality theory has important applications; as a striking example, one could mention the following result of H. Whitney: A graph
. The duality theory has important applications; as a striking example, one could mention the following result of H. Whitney: A graph 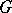 with associated graphic matroid
with associated graphic matroid 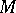 (determined by the circuits, respectively forests, of
(determined by the circuits, respectively forests, of 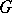 as above) is planar if and only if the dual matroid
as above) is planar if and only if the dual matroid 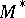 is also graphic.
is also graphic.
Matroids are also studied from a more geometric point of view, under the name "combinatorial geometries" (cf. also Combinatorial geometry).
Finally, it is also possible to define matroids in an algorithmic way. Let 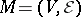 be a set system satisfying conditions 1) and 2) above and consider a weighting on
be a set system satisfying conditions 1) and 2) above and consider a weighting on 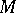 , i.e. a mapping
, i.e. a mapping 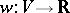 into the real numbers satisfying
into the real numbers satisfying 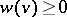 for all
for all 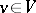 . One extends
. One extends 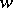 to the power set of
to the power set of 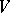 by putting
by putting 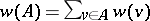 for each subset
for each subset 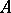 of
of 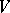 . It is required to find a subset
. It is required to find a subset 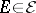 of maximal weight (among all subsets in
of maximal weight (among all subsets in 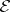 ). Then
). Then 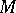 is a matroid if and only if the greedy algorithm solves this problem for every weighting
is a matroid if and only if the greedy algorithm solves this problem for every weighting 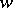 : One orders the elements of
: One orders the elements of 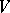 according to weight, say
according to weight, say 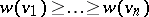 and determines
and determines 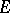 (starting from the empty set) recursively as follows: In step
(starting from the empty set) recursively as follows: In step 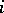 , the element
, the element 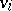 is added to
is added to 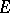 unless this results in a set no longer contained in
unless this results in a set no longer contained in 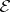 . Due to this algorithmic property, matroids are an extremely important tool in combinatorial optimization.
. Due to this algorithmic property, matroids are an extremely important tool in combinatorial optimization.
Matroids are also used in the stratification of Grassmann manifolds, in the analysis of higher-dimensional splines and 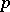 -adic curves, and in many other areas.
-adic curves, and in many other areas.
An important related concept is that of an oriented matroid, which is an abstraction of a linear algebra over an ordered field, and is used in the study of convex polytopes.
The seminal paper that started the whole theory of matroids is [1] (also included in [a8]).
References
| [a1] | D.J.A. Welsh, "Matroid theory" , Acad. Press (1976); reprinted (Courier Dover Publications, 2010) ISBN 9780486474397 |
| [a2] | E.L. Lawler, "Combinatorial optimization: networks and matroids" , Holt, Rinehart & Winston (1976) |
| [a3] | C.H. Papadimitriou, K. Steiglitz, "Combinatorial optimization. Algorithms and complexity" , Prentice-Hall (1982) |
| [a4] | Neil White (ed.) , Theory of matroids , Cambridge Univ. Press (1986) |
| [a5] | Neil White (ed.) , Combinatorial geometries, Encyclopedia of Mathematics and its Applications 29. Cambridge Univ. Press (1987) ISBN 0-521-33339-3, Zbl 0626.00007 |
| [a6] | Neil White (ed.) , Combinatorial geometries: Advanced theory , Cambridge Univ. Press (1986) |
| [a7] | M. Aigner, "Kombinatorik II. Matroide und Transversaltheorie" , Springer (1976) |
| [a8] | J.P.S. Kung, "A source book in matroid theory" , Birkhäuser (1986) |
| [a9] | Oxley, James G. Matroid theory. Oxford Science Publications. Oxford: Oxford University Press (1992). ISBN 0-19-853563-5, Zbl 0784.05002 |
Greedoid
A generalisation of the concept of matroid. A greedoid on a set $V$ is a set system $\mathcal{F}$ of subset of $V$, called "feasible" sets, with the properties: 1) the empty set is feasible, $\emptyset \in \mathcal{F}$; 2) if $F \in \mathcal{F}$ is non-empty, then there is $x \in F$ such that $F \setminus \{x\} \in \mathcal{F}$; 3) if $X, Y \in \mathcal{F}$ with $|X| > |Y|$ then there is $x \in X$ such that $Y \cup \{x\} \in \mathcal{F}$.
Axiom (3), the exchange property, implies that all maximal feasible sets have the same number of elements. The independent sets of a matroid form a greedoid, and the feasible sets of a greedoid form a matroid if they are hereditary, that is, axiom (2) holds in the strong form that for every $x \in F$, $F \setminus \{x\} \in \mathcal{F}$.
References
- Björner, Anders; Ziegler, Günter M. "Introduction to greedoids", Matroid applications, ed Neil White, Encycl. Math. Appl. 40, Cambridge University Press (1992) 284-357. ISBN 0-521-38165-7 Zbl 0772.05026
Matroid. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Matroid&oldid=34627