Difference between revisions of "Ellipsoidal coordinates"
From Encyclopedia of Mathematics
(Importing text file) |
(→References: Jeffreys & Jeffreys (1972)) |
||
| Line 33: | Line 33: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> G. Darboux, "Leçons sur la théorie générale des surfaces et ses applications géométriques du calcul infinitésimal" , '''1''' , Gauthier-Villars (1887) pp. 1–18</TD></TR></table> | + | <table> |
| + | <TR><TD valign="top">[a1]</TD> <TD valign="top"> G. Darboux, "Leçons sur la théorie générale des surfaces et ses applications géométriques du calcul infinitésimal" , '''1''' , Gauthier-Villars (1887) pp. 1–18</TD></TR> | ||
| + | <TR><TD valign="top">[a2]</TD> <TD valign="top"> Harold Jeffreys, Bertha Jeffreys, ''Methods of Mathematical Physics'', 3rd edition, Cambridge University Press (1972) Zbl 0238.00004</TD></TR> | ||
| + | </table> | ||
Revision as of 20:14, 25 October 2014
spatial elliptic coordinates
The numbers 
, 
and 
connected with Cartesian rectangular coordinates 
, 
and 
by the formulas
 |
 |
 |
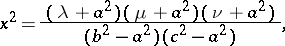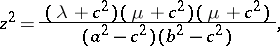where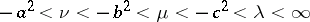 
. The coordinate surfaces are (see Fig.): ellipses 
, one-sheet hyperbolas (
), and two-sheet hyperbolas (
), with centres at the coordinate origin.
Figure: e035420a
The system of ellipsoidal coordinates is orthogonal. To every triple of numbers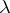 
, 
and 
correspond 8 points (one in each octant), which are symmetric to each other relative to the coordinate planes of the system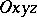 
.
The Lamé coefficients are
 |
 |
 |
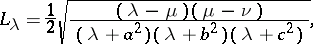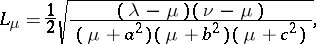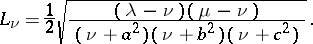If one of the conditions 
in the definition of ellipsoidal coordinates is replaced by an equality, then degenerate ellipsoidal coordinate systems are obtained.
Comments
References
| [a1] | G. Darboux, "Leçons sur la théorie générale des surfaces et ses applications géométriques du calcul infinitésimal" , 1 , Gauthier-Villars (1887) pp. 1–18 |
| [a2] | Harold Jeffreys, Bertha Jeffreys, Methods of Mathematical Physics, 3rd edition, Cambridge University Press (1972) Zbl 0238.00004 |
How to Cite This Entry:
Ellipsoidal coordinates. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ellipsoidal_coordinates&oldid=34026
Ellipsoidal coordinates. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ellipsoidal_coordinates&oldid=34026
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article