Difference between revisions of "Quaternionic structure"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
|||
| Line 5: | Line 5: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679034.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679034.png" /></td> </tr></table> | ||
| − | A quaternionic structure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679035.png" /> on a manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679036.png" /> is induced by a special quaternionic structure if and only if the bundle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679037.png" /> is trivial. A quaternionic structure on a manifold can be regarded as a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679038.png" />-structure, and a special quaternionic structure as a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679039.png" />-structure in the sense of the theory of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679040.png" />-structures (cf. [[G-structure | + | A quaternionic structure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679035.png" /> on a manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679036.png" /> is induced by a special quaternionic structure if and only if the bundle <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679037.png" /> is trivial. A quaternionic structure on a manifold can be regarded as a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679038.png" />-structure, and a special quaternionic structure as a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679039.png" />-structure in the sense of the theory of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679040.png" />-structures (cf. [[G-structure|<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679041.png" />-structure]]). Hence, in order that a quaternionic structure (or a special quaternionic structure) should exist on a manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679042.png" />, it is necessary and sufficient that the structure group of the tangent bundle reduces to the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679043.png" /> (or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679044.png" />). The first prolongation of a special quaternionic structure, regarded as a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679045.png" />-structure, is an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679046.png" />-structure (a field of frames), which determines a canonical [[Linear connection|linear connection]] associated with the special quaternionic structure. The vanishing of the [[Curvature|curvature]] and [[Torsion|torsion]] of this connection is a necessary and sufficient condition for the special quaternionic structure to be locally equivalent to the standard flat special quaternionic structure on the vector space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679047.png" />. |
A quaternionic Riemannian manifold is the analogue of a [[Kähler manifold|Kähler manifold]] for quaternionic structures. It is defined as a [[Riemannian manifold|Riemannian manifold]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679048.png" /> of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679049.png" /> whose holonomy group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679050.png" /> is contained in the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679051.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679052.png" />, then the quaternionic Riemannian manifold is called a special or quaternionic Kähler manifold, and it has zero [[Ricci curvature|Ricci curvature]]. A quaternionic Riemannian manifold can be characterized as a Riemannian manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679053.png" /> in which there exists a quaternionic structure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679054.png" /> that is invariant with respect to Levi-Civita [[Parallel displacement(2)|parallel displacement]]. Similarly, a special quaternionic Riemannian manifold is a Riemannian manifold in which there exists a special quaternionic structure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679055.png" /> that is invariant with respect to Levi-Civita parallel displacement: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679056.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679057.png" /> is the operator of [[Covariant differentiation|covariant differentiation]] of the [[Levi-Civita connection|Levi-Civita connection]]. | A quaternionic Riemannian manifold is the analogue of a [[Kähler manifold|Kähler manifold]] for quaternionic structures. It is defined as a [[Riemannian manifold|Riemannian manifold]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679048.png" /> of dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679049.png" /> whose holonomy group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679050.png" /> is contained in the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679051.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679052.png" />, then the quaternionic Riemannian manifold is called a special or quaternionic Kähler manifold, and it has zero [[Ricci curvature|Ricci curvature]]. A quaternionic Riemannian manifold can be characterized as a Riemannian manifold <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679053.png" /> in which there exists a quaternionic structure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679054.png" /> that is invariant with respect to Levi-Civita [[Parallel displacement(2)|parallel displacement]]. Similarly, a special quaternionic Riemannian manifold is a Riemannian manifold in which there exists a special quaternionic structure <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679055.png" /> that is invariant with respect to Levi-Civita parallel displacement: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679056.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/q/q076/q076790/q07679057.png" /> is the operator of [[Covariant differentiation|covariant differentiation]] of the [[Levi-Civita connection|Levi-Civita connection]]. | ||
Revision as of 08:30, 19 October 2014
A quaternionic structure on a real vector space 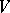 is a module structure over the skew-field of quaternions
is a module structure over the skew-field of quaternions  , that is, a subalgebra
, that is, a subalgebra 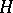 of the algebra
of the algebra 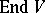 of endomorphisms of
of endomorphisms of 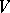 induced by two anti-commutative complex structures
induced by two anti-commutative complex structures 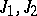 on
on 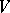 (cf. Complex structure). The endomorphisms
(cf. Complex structure). The endomorphisms 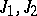 are called standard generators of the quaternionic structure
are called standard generators of the quaternionic structure 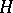 , and the basis
, and the basis 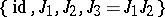 of
of 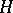 defined by them is called the standard basis. A standard basis is defined up to automorphisms of
defined by them is called the standard basis. A standard basis is defined up to automorphisms of 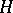 . The algebra
. The algebra 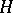 is isomorphic to the algebra of quaternions (cf. Quaternion). An automorphism
is isomorphic to the algebra of quaternions (cf. Quaternion). An automorphism 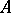 of the vector space
of the vector space 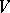 is called an automorphism of the quaternionic structure if the transformation
is called an automorphism of the quaternionic structure if the transformation 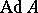 of the space of automorphisms induced by it preserves
of the space of automorphisms induced by it preserves  , that is, if
, that is, if 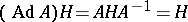 . If, moreover, the identity automorphism is induced on
. If, moreover, the identity automorphism is induced on 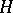 , then
, then 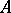 is called a special automorphism of the quaternionic structure. The group of all special automorphisms of the quaternionic structure is isomorphic to the general linear group
is called a special automorphism of the quaternionic structure. The group of all special automorphisms of the quaternionic structure is isomorphic to the general linear group 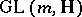 over the skew-field
over the skew-field  , where
, where 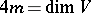 . The group of all automorphisms of a quaternionic structure is isomorphic to the direct product with amalgamation of the subgroup
. The group of all automorphisms of a quaternionic structure is isomorphic to the direct product with amalgamation of the subgroup 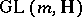 and the group of unit quaternions
and the group of unit quaternions 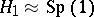 .
.
A quaternionic structure on a differentiable manifold is a field of quaternionic structures on the tangent spaces, that is, a subbundle 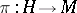 of the bundle
of the bundle 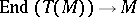 of endomorphisms of tangent spaces whose fibres
of endomorphisms of tangent spaces whose fibres 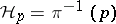 are quaternionic structures on the tangent spaces
are quaternionic structures on the tangent spaces 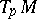 for all
for all 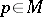 . A pair of anti-commutative almost-complex structures
. A pair of anti-commutative almost-complex structures 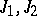 on the manifold
on the manifold 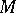 is called a special quaternionic structure. It induces the quaternionic structure
is called a special quaternionic structure. It induces the quaternionic structure 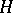 , where
, where
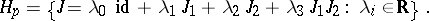 |
A quaternionic structure 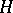 on a manifold
on a manifold 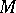 is induced by a special quaternionic structure if and only if the bundle
is induced by a special quaternionic structure if and only if the bundle 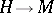 is trivial. A quaternionic structure on a manifold can be regarded as a
is trivial. A quaternionic structure on a manifold can be regarded as a 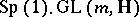 -structure, and a special quaternionic structure as a
-structure, and a special quaternionic structure as a 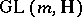 -structure in the sense of the theory of
-structure in the sense of the theory of 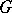 -structures (cf.
-structures (cf. 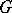 -structure). Hence, in order that a quaternionic structure (or a special quaternionic structure) should exist on a manifold
-structure). Hence, in order that a quaternionic structure (or a special quaternionic structure) should exist on a manifold 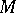 , it is necessary and sufficient that the structure group of the tangent bundle reduces to the group
, it is necessary and sufficient that the structure group of the tangent bundle reduces to the group 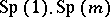 (or
(or 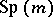 ). The first prolongation of a special quaternionic structure, regarded as a
). The first prolongation of a special quaternionic structure, regarded as a 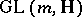 -structure, is an
-structure, is an  -structure (a field of frames), which determines a canonical linear connection associated with the special quaternionic structure. The vanishing of the curvature and torsion of this connection is a necessary and sufficient condition for the special quaternionic structure to be locally equivalent to the standard flat special quaternionic structure on the vector space
-structure (a field of frames), which determines a canonical linear connection associated with the special quaternionic structure. The vanishing of the curvature and torsion of this connection is a necessary and sufficient condition for the special quaternionic structure to be locally equivalent to the standard flat special quaternionic structure on the vector space 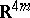 .
.
A quaternionic Riemannian manifold is the analogue of a Kähler manifold for quaternionic structures. It is defined as a Riemannian manifold 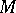 of dimension
of dimension 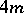 whose holonomy group
whose holonomy group 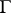 is contained in the group
is contained in the group 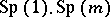 . If
. If 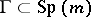 , then the quaternionic Riemannian manifold is called a special or quaternionic Kähler manifold, and it has zero Ricci curvature. A quaternionic Riemannian manifold can be characterized as a Riemannian manifold
, then the quaternionic Riemannian manifold is called a special or quaternionic Kähler manifold, and it has zero Ricci curvature. A quaternionic Riemannian manifold can be characterized as a Riemannian manifold 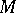 in which there exists a quaternionic structure
in which there exists a quaternionic structure 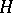 that is invariant with respect to Levi-Civita parallel displacement. Similarly, a special quaternionic Riemannian manifold is a Riemannian manifold in which there exists a special quaternionic structure
that is invariant with respect to Levi-Civita parallel displacement. Similarly, a special quaternionic Riemannian manifold is a Riemannian manifold in which there exists a special quaternionic structure 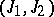 that is invariant with respect to Levi-Civita parallel displacement:
that is invariant with respect to Levi-Civita parallel displacement: 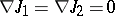 , where
, where  is the operator of covariant differentiation of the Levi-Civita connection.
is the operator of covariant differentiation of the Levi-Civita connection.
In a quaternionic Riemannian manifold there exists a canonical parallel 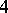 -form that defines a number of operators in the ring
-form that defines a number of operators in the ring 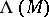 of differential forms on
of differential forms on 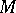 that commute with the Laplace–Beltrami operator (exterior product operator, contraction operators). This enables one to construct an interesting theory of harmonic differential forms on quaternionic Riemannian manifolds [2] analogous to Hodge theory for Kähler manifolds, and to obtain estimates for the Betti numbers of the manifold
that commute with the Laplace–Beltrami operator (exterior product operator, contraction operators). This enables one to construct an interesting theory of harmonic differential forms on quaternionic Riemannian manifolds [2] analogous to Hodge theory for Kähler manifolds, and to obtain estimates for the Betti numbers of the manifold 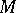 (cf. Hodge structure; Betti number). Locally Euclidean spaces account for all the homogeneous special quaternionic Riemannian manifolds. As an example of a homogeneous quaternionic Riemannian manifold that is not special one may cite the quaternionic projective space and also other Wolf symmetric spaces which are in one-to-one correspondence with simple compact Lie groups without centre (cf. Symmetric space). These account for all compact homogeneous quaternionic Riemannian manifolds. A wide class of non-compact non-symmetric homogeneous quaternionic Riemannian manifolds can be constructed by means of modules over Clifford algebras (see [5]).
(cf. Hodge structure; Betti number). Locally Euclidean spaces account for all the homogeneous special quaternionic Riemannian manifolds. As an example of a homogeneous quaternionic Riemannian manifold that is not special one may cite the quaternionic projective space and also other Wolf symmetric spaces which are in one-to-one correspondence with simple compact Lie groups without centre (cf. Symmetric space). These account for all compact homogeneous quaternionic Riemannian manifolds. A wide class of non-compact non-symmetric homogeneous quaternionic Riemannian manifolds can be constructed by means of modules over Clifford algebras (see [5]).
References
| [1] | S.-S. Chern, "On a generalization of Kähler geometry" R.H. Fox (ed.) D.C. Spencer (ed.) A.W. Tucker (ed.) , Algebraic geometry and topology (Symp. in honor of S. Lefschetz) , Princeton Univ. Press (1957) pp. 103–121 MR0087172 Zbl 0078.14103 |
| [2] | V.Y. Kraines, "Topology of quaternionic manifolds" Trans. Amer. Math. Soc. , 122 (1966) pp. 357–367 MR0192513 Zbl 0148.16101 |
| [3] | K. Yano, M. Ako, "An affine connection in an almost quaternionic manifold" J. Differential Geom. , 8 : 3 (1973) pp. 341–347 MR355892 |
| [4] | A.J. Sommese, "Quaternionic manifolds" Mat. Ann. , 212 (1975) pp. 191–214 MR0425827 Zbl 0299.53023 |
| [5] | D.V. Alekseevskii, "Classification of quaternionic spaces with a transitive solvable group of motions" Math. USSR Izv. , 9 : 2 (1975) pp. 297–339 Izv. Akad. Nauk SSSR Ser. Mat. , 39 : 2 (1975) pp. 315–362 MR402649 Zbl 0324.53038 |
| [6] | J.A. Wolf, "Complex homogeneous contact manifolds and quaternionic symmetric spaces" J. Math. Mech. , 14 : 6 (1965) pp. 1033–1047 MR0185554 Zbl 0141.38202 |
| [7] | D.V. Aleksevskii, "Lie groups and homogeneous spaces" J. Soviet Math. , 4 : 5 (1975) pp. 483–539 Itogi Nauk. i Tekhn. Algebra. Topol. Geom. , 11 (1974) pp. 37–123 |
Quaternionic structure. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quaternionic_structure&oldid=33885