Difference between revisions of "Acceleration of convergence"
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| + | {{TEX|done}} | ||
''(for an iterative method)'' | ''(for an iterative method)'' | ||
The construction of a modification of the iterative method, by means of that method, that possesses a greater [[Rate of convergence|rate of convergence]]. The acceleration methods (acceleration processes) used are quite varied (see [[#References|[1]]]–[[#References|[6]]]) and depend both on the problem to be solved and on the type of iterative method. In those cases where the iterative method can be considered as a particular case of a class of iterative methods containing free iteration parameters, acceleration of convergence can be reduced to the problem of the optimal choice of these parameters. The optimization problem can take various forms, and may reduce, for example, to a transition from a method of simple iteration, | The construction of a modification of the iterative method, by means of that method, that possesses a greater [[Rate of convergence|rate of convergence]]. The acceleration methods (acceleration processes) used are quite varied (see [[#References|[1]]]–[[#References|[6]]]) and depend both on the problem to be solved and on the type of iterative method. In those cases where the iterative method can be considered as a particular case of a class of iterative methods containing free iteration parameters, acceleration of convergence can be reduced to the problem of the optimal choice of these parameters. The optimization problem can take various forms, and may reduce, for example, to a transition from a method of simple iteration, | ||
| − | + | $$u^{n+1}=u^n-\tau(Lu^n-f),\tag{1}$$ | |
for the solution of a system of linear algebraic equations | for the solution of a system of linear algebraic equations | ||
| − | + | $$Lu=f,\quad L=L^*>0,\tag{2}$$ | |
| − | either to the Richardson method with Chebyshev parameters or to the method of conjugate gradients. The rate of convergence of similar classical iterative methods depends on the condition number | + | either to the Richardson method with Chebyshev parameters or to the method of conjugate gradients. The rate of convergence of similar classical iterative methods depends on the condition number $\nu(L)$ of the matrix $L$ and can be fairly slow for large $\nu(L)$. In such situations, and particularly for the solution of systems of grid equations, modifications of these methods are often used, these can be defined by the fact that they are used not for \ref{2}, but for an equivalent system |
| − | + | $$B^{-1}Lu=B^{-1}f,$$ | |
| − | where | + | where $B=B^*>0$ is a specially selected operator (see [[#References|[2]]]–[[#References|[4]]]). |
| − | The operator | + | The operator $B^{-1}L$ is self-adjoint and positive on some Euclidean space and the rate of convergence of the modifications obtained depends on $\nu(B^{-1}L)$. Similar modifications are also used for more general problems, including non-linear problems (see [[Non-linear equation, numerical methods|Non-linear equation, numerical methods]]). In order to realise these modifications it is important to be able to solve the systems $Bv=g$ effectively, since, for example, modification of \ref{1} leads to the relation |
| − | + | $$u^{n+1}=u^n-\tau B^{-1}(Lu^n-f)\tag{3}$$ | |
(see [[Minimization of the labour of calculation|Minimization of the labour of calculation]]). | (see [[Minimization of the labour of calculation|Minimization of the labour of calculation]]). | ||
| − | One of the traditional general methods for the acceleration of convergence for methods | + | One of the traditional general methods for the acceleration of convergence for methods \ref{1} is the $\delta^2$-process. It is used along with a whole series of other acceleration methods (see [[#References|[1]]]) in iterative methods for the partial eigen value problem. |
In solving non-linear problems, acceleration of convergence is often achieved by choosing a special initial approximation on the basis of methods of continuation by a parameter. For these same problems acceleration of convergence is also sometimes realized by the use of iterative methods of a higher order (the Newton–Kantorovich method and others). | In solving non-linear problems, acceleration of convergence is often achieved by choosing a special initial approximation on the basis of methods of continuation by a parameter. For these same problems acceleration of convergence is also sometimes realized by the use of iterative methods of a higher order (the Newton–Kantorovich method and others). | ||
| Line 33: | Line 34: | ||
====Comments==== | ====Comments==== | ||
| − | In the Western literature, Richardson's method with Chebyshev parameters is usually called the Chebyshev semi-iterative method. Chebyshev iteration is extensively analyzed in [[#References|[a3]]] and [[#References|[a7]]], Chapt. 5. A further analysis for the case when | + | In the Western literature, Richardson's method with Chebyshev parameters is usually called the Chebyshev semi-iterative method. Chebyshev iteration is extensively analyzed in [[#References|[a3]]] and [[#References|[a7]]], Chapt. 5. A further analysis for the case when $L$ is non-symmetric can be found in [[#References|[a4]]]. |
| − | Unlike Chebyshev iteration, the method of conjugate gradients does not need accurate estimates of the largest and smallest eigen values of the iteration matrix | + | Unlike Chebyshev iteration, the method of conjugate gradients does not need accurate estimates of the largest and smallest eigen values of the iteration matrix $I-\tau L$ in \ref{1}. Good references are [[#References|[a2]]], pp. 362-379, and [[#References|[a6]]]. Further developments are discussed in [[#References|[a5]]]. |
| − | The pre-multiplication by a matrix | + | The pre-multiplication by a matrix $B^{-1}$ of the system \ref{2} is often called pre-conditioning. An up-to-date survey of this technique is given in [[#References|[a1]]]. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> O. Axelsson, "Conjugate gradient type methods for unsymmetric and inconsistent systems of linear equations" ''Linear algebra and its Appl.'' , '''34''' (1980) pp. 1–66</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> G.H. Golub, C.F. van Loan, "Matrix computations" , North Oxford Acad. (1983)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> G.H. Golub, R.S. Varga, "Chebyshev semi-iterative methods, successive over-relaxation methods, and second-order Richardson iterative methods. Part I, II" ''Numerical Math.'' , '''3''' (1961) pp. 147–156; 157–168</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> T.A. Manteuffel, "The Tchebychev iteration for nonsymmetric linear systems" ''Numerical Math.'' , '''28''' (1977) pp. 307–327</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> J.A. Meijerink, H.A. van der Vorst, "An iterative solution method for linear systems of which the coefficient matrix is a symmetric <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010510/a01051017.png" />-matrix" ''Math. Comp.'' , '''31''' (1977) pp. 148–162</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> G.W. Stewart, "Conjugate gradients methods for solving systems of linear equations" ''Numerical Math.'' , '''21''' (1973) pp. 284–297</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> R.S. Varga, "Matrix iterative analysis" , Prentice-Hall (1962)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> O. Axelsson, "Conjugate gradient type methods for unsymmetric and inconsistent systems of linear equations" ''Linear algebra and its Appl.'' , '''34''' (1980) pp. 1–66</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> G.H. Golub, C.F. van Loan, "Matrix computations" , North Oxford Acad. (1983)</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> G.H. Golub, R.S. Varga, "Chebyshev semi-iterative methods, successive over-relaxation methods, and second-order Richardson iterative methods. Part I, II" ''Numerical Math.'' , '''3''' (1961) pp. 147–156; 157–168</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> T.A. Manteuffel, "The Tchebychev iteration for nonsymmetric linear systems" ''Numerical Math.'' , '''28''' (1977) pp. 307–327</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> J.A. Meijerink, H.A. van der Vorst, "An iterative solution method for linear systems of which the coefficient matrix is a symmetric <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a010/a010510/a01051017.png" />-matrix" ''Math. Comp.'' , '''31''' (1977) pp. 148–162</TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> G.W. Stewart, "Conjugate gradients methods for solving systems of linear equations" ''Numerical Math.'' , '''21''' (1973) pp. 284–297</TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> R.S. Varga, "Matrix iterative analysis" , Prentice-Hall (1962)</TD></TR></table> | ||
Revision as of 13:55, 16 October 2014
(for an iterative method)
The construction of a modification of the iterative method, by means of that method, that possesses a greater rate of convergence. The acceleration methods (acceleration processes) used are quite varied (see [1]–[6]) and depend both on the problem to be solved and on the type of iterative method. In those cases where the iterative method can be considered as a particular case of a class of iterative methods containing free iteration parameters, acceleration of convergence can be reduced to the problem of the optimal choice of these parameters. The optimization problem can take various forms, and may reduce, for example, to a transition from a method of simple iteration,
$$u^{n+1}=u^n-\tau(Lu^n-f),\tag{1}$$
for the solution of a system of linear algebraic equations
$$Lu=f,\quad L=L^*>0,\tag{2}$$
either to the Richardson method with Chebyshev parameters or to the method of conjugate gradients. The rate of convergence of similar classical iterative methods depends on the condition number $\nu(L)$ of the matrix $L$ and can be fairly slow for large $\nu(L)$. In such situations, and particularly for the solution of systems of grid equations, modifications of these methods are often used, these can be defined by the fact that they are used not for \ref{2}, but for an equivalent system
$$B^{-1}Lu=B^{-1}f,$$
where $B=B^*>0$ is a specially selected operator (see [2]–[4]).
The operator $B^{-1}L$ is self-adjoint and positive on some Euclidean space and the rate of convergence of the modifications obtained depends on $\nu(B^{-1}L)$. Similar modifications are also used for more general problems, including non-linear problems (see Non-linear equation, numerical methods). In order to realise these modifications it is important to be able to solve the systems $Bv=g$ effectively, since, for example, modification of \ref{1} leads to the relation
$$u^{n+1}=u^n-\tau B^{-1}(Lu^n-f)\tag{3}$$
(see Minimization of the labour of calculation).
One of the traditional general methods for the acceleration of convergence for methods \ref{1} is the $\delta^2$-process. It is used along with a whole series of other acceleration methods (see [1]) in iterative methods for the partial eigen value problem.
In solving non-linear problems, acceleration of convergence is often achieved by choosing a special initial approximation on the basis of methods of continuation by a parameter. For these same problems acceleration of convergence is also sometimes realized by the use of iterative methods of a higher order (the Newton–Kantorovich method and others).
Various methods for the acceleration of convergence are also used in probabilistic iterative methods of Monte-Carlo type (see [2]).
References
| [1] | D.K. Faddeev, V.N. Faddeeva, "Computational methods of linear algebra" , Freeman (1963) (Translated from Russian) |
| [2] | N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian) |
| [3] | G.I. Marchuk, "Methods of numerical mathematics" , Springer (1982) (Translated from Russian) |
| [4] | A.A. Samarskii, E.S. Nikolaev, "Numerical methods for grid equations" , 1–2 , Birkhäuser (1989) (Translated from Russian) |
| [5] | R. Glowinski, "Numerical methods for nonlinear variational problems" , Springer (1984) |
| [6] | E.G. D'yakonov, "On iterative methods with saddle operators" Dokl. Akad. Nauk. SSSR, New Series , 292 (1987) pp. 1037–1041 (In Russian) |
Comments
In the Western literature, Richardson's method with Chebyshev parameters is usually called the Chebyshev semi-iterative method. Chebyshev iteration is extensively analyzed in [a3] and [a7], Chapt. 5. A further analysis for the case when $L$ is non-symmetric can be found in [a4].
Unlike Chebyshev iteration, the method of conjugate gradients does not need accurate estimates of the largest and smallest eigen values of the iteration matrix $I-\tau L$ in \ref{1}. Good references are [a2], pp. 362-379, and [a6]. Further developments are discussed in [a5].
The pre-multiplication by a matrix $B^{-1}$ of the system \ref{2} is often called pre-conditioning. An up-to-date survey of this technique is given in [a1].
References
| [a1] | O. Axelsson, "Conjugate gradient type methods for unsymmetric and inconsistent systems of linear equations" Linear algebra and its Appl. , 34 (1980) pp. 1–66 |
| [a2] | G.H. Golub, C.F. van Loan, "Matrix computations" , North Oxford Acad. (1983) |
| [a3] | G.H. Golub, R.S. Varga, "Chebyshev semi-iterative methods, successive over-relaxation methods, and second-order Richardson iterative methods. Part I, II" Numerical Math. , 3 (1961) pp. 147–156; 157–168 |
| [a4] | T.A. Manteuffel, "The Tchebychev iteration for nonsymmetric linear systems" Numerical Math. , 28 (1977) pp. 307–327 |
| [a5] | J.A. Meijerink, H.A. van der Vorst, "An iterative solution method for linear systems of which the coefficient matrix is a symmetric 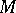 -matrix" Math. Comp. , 31 (1977) pp. 148–162 -matrix" Math. Comp. , 31 (1977) pp. 148–162 |
| [a6] | G.W. Stewart, "Conjugate gradients methods for solving systems of linear equations" Numerical Math. , 21 (1973) pp. 284–297 |
| [a7] | R.S. Varga, "Matrix iterative analysis" , Prentice-Hall (1962) |
Acceleration of convergence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Acceleration_of_convergence&oldid=33676