Difference between revisions of "Method of characteristics"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
(TeX) |
||
| Line 1: | Line 1: | ||
| + | {{TEX|done}} | ||
A method for the numerical integration of equations of hyperbolic type. In the domain of hyperbolicity there is a linear combination of initial equations in which there occur only interior derivatives along characteristic surfaces. Then the equations to be solved simplify substantially. In the method of characteristics the solution is computed on a characteristic grid, which is constructed in the process of calculation, and so the domain of dependency of the solution can be determined exactly. For the method of characteristics the existence of a solution and its convergence have been proved. The widest application of the method of characteristics is in the solution of problems of the mechanics of continuous media (see [[#References|[1]]]). For example, the equations in characteristic form | A method for the numerical integration of equations of hyperbolic type. In the domain of hyperbolicity there is a linear combination of initial equations in which there occur only interior derivatives along characteristic surfaces. Then the equations to be solved simplify substantially. In the method of characteristics the solution is computed on a characteristic grid, which is constructed in the process of calculation, and so the domain of dependency of the solution can be determined exactly. For the method of characteristics the existence of a solution and its convergence have been proved. The widest application of the method of characteristics is in the solution of problems of the mechanics of continuous media (see [[#References|[1]]]). For example, the equations in characteristic form | ||
| − | + | $$\frac{\partial J}{\partial t}+\frac{p}{\rho^2}\frac{\partial\rho}{\partial t}+u\frac{\partial J}{\partial t}-\frac{p}{\rho^2}\frac{\partial\rho}{\partial x}=0,\tag{1}$$ | |
| − | + | $$\frac{\partial p}{\partial t}+(u\pm c)\frac{\partial p}{\partial x}\pm\rho c\left(\frac{\partial u}{\partial t}+(u\pm c)\frac{\partial u}{\partial x}\right)=0\tag{2}$$ | |
| − | are a linear combination of the traditional equations of gas dynamics: continuity, momentum and energy. Here and below | + | are a linear combination of the traditional equations of gas dynamics: continuity, momentum and energy. Here and below $\rho$ is the density, $u$ is the velocity, $J$ is the intrinsic energy of a unit mass, $p=p(\rho,J)$ is the pressure, $T$ is the temperature, $x$ is the spatial coordinate, and $t$ is the time. The Cauchy problem asks for a solution in the domain $t>0$ for given data on the line $t=0$. Entropy is the name for an integral $S(\rho,J)=\text{const}$ of the equation |
| − | + | $$dJ-\frac{p(\rho,J)}{\rho^2}d\rho=0.$$ | |
| − | Then | + | Then \ref{1} has the form |
| − | + | $$\frac{\partial S}{\partial t}+u\frac{\partial S}{\partial x}=0.\tag{1prm}$$ | |
| − | On the left-hand sides of | + | On the left-hand sides of \ref{1prm} and \ref{2} there stand the derivatives $dS/dt$, $dp/dt$, $du/dt$, taken in the directions |
| − | + | $$\frac{dx}{dt}=u\tag{3}$$ | |
and | and | ||
| − | + | $$\frac{dx}{dt}=u\pm c,\tag{4}$$ | |
| − | the so-called characteristics. The system | + | the so-called characteristics. The system \ref{1}, \ref{2} has three families of real characteristics. Along the characteristics \ref{3} the relation |
| − | + | $$dS=0$$ | |
| − | holds, and along the characteristic | + | holds, and along the characteristic \ref{4} the relations |
| − | + | $$dp\pm\rho cdu=0\tag{5}$$ | |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/m063580a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/m063580a.gif" /> | ||
| Line 33: | Line 34: | ||
Figure: m063580a | Figure: m063580a | ||
| − | hold. Through the point | + | hold. Through the point $A$ (see Fig.) there passes a characteristic \ref{4} on the side of increasing $t$, |
| − | + | $$\frac{x-x_A}{t-t_A}=u_A+c_A.$$ | |
| − | Through a point close to | + | Through a point close to $A$ on the right, say $B$, there passes a characteristic \ref{4} of another family |
| − | + | $$\frac{x-x_B}{t-t_B}=u_B-c_B,$$ | |
| − | where | + | where $C$ is the point of intersection of the characteristics. When one replaces the differential relations \ref{5}, which hold along characteristics, by differences, one obtains the algebraic system |
| − | + | $$(p_C-p_A)+\rho_Ac_A(u_C-u_A)=0,$$ | |
| − | + | $$(p_C-p_B)-\rho_Bc_B(u_C-u_B)=0,$$ | |
| − | from which | + | from which $p_C$ and $u_C$ can be determined. From $C$ one draws the characteristic \ref{3}, |
| − | + | $$\frac{x-x_C}{t-t_C}=u_C,$$ | |
| − | up to the intersection with | + | up to the intersection with $AB$ at $D$. The value of the entropy $S$ at $D$ is determined by means of interpolation between the points $A$ and $B$ (here $S_C=S_D$). From the equations |
| − | + | $$p(\rho_C,J_C)=p_C,$$ | |
| − | + | $$S(\rho_C,J_C)=S_C$$ | |
| − | one can find the values of the intrinsic energy | + | one can find the values of the intrinsic energy $J_C$ and the density $\rho_C$ at $C$. When the data at the two points $A$ and $D$ are known, one can find the solution at $C$ for large values of $t$. This procedure of computations is repeated for every pair of points. Then, by using new points $C$ instead of the original $A$ and $B$, one takes the next step in $t$. The calculation is made for the required values of $t$. However, since the equations of gas dynamics are non-linear, the calculation may come to a stop at a certain moment of time if the characteristics of one family touch each other or intersect. |
The difference scheme thus described is of the first order of accuracy (an analogue of Euler's method of polygonal lines for solving ordinary differential equations). An increase in accuracy can be achieved by repetitions of the calculations, etc. | The difference scheme thus described is of the first order of accuracy (an analogue of Euler's method of polygonal lines for solving ordinary differential equations). An increase in accuracy can be achieved by repetitions of the calculations, etc. | ||
Revision as of 13:50, 4 October 2014
A method for the numerical integration of equations of hyperbolic type. In the domain of hyperbolicity there is a linear combination of initial equations in which there occur only interior derivatives along characteristic surfaces. Then the equations to be solved simplify substantially. In the method of characteristics the solution is computed on a characteristic grid, which is constructed in the process of calculation, and so the domain of dependency of the solution can be determined exactly. For the method of characteristics the existence of a solution and its convergence have been proved. The widest application of the method of characteristics is in the solution of problems of the mechanics of continuous media (see [1]). For example, the equations in characteristic form
$$\frac{\partial J}{\partial t}+\frac{p}{\rho^2}\frac{\partial\rho}{\partial t}+u\frac{\partial J}{\partial t}-\frac{p}{\rho^2}\frac{\partial\rho}{\partial x}=0,\tag{1}$$
$$\frac{\partial p}{\partial t}+(u\pm c)\frac{\partial p}{\partial x}\pm\rho c\left(\frac{\partial u}{\partial t}+(u\pm c)\frac{\partial u}{\partial x}\right)=0\tag{2}$$
are a linear combination of the traditional equations of gas dynamics: continuity, momentum and energy. Here and below $\rho$ is the density, $u$ is the velocity, $J$ is the intrinsic energy of a unit mass, $p=p(\rho,J)$ is the pressure, $T$ is the temperature, $x$ is the spatial coordinate, and $t$ is the time. The Cauchy problem asks for a solution in the domain $t>0$ for given data on the line $t=0$. Entropy is the name for an integral $S(\rho,J)=\text{const}$ of the equation
$$dJ-\frac{p(\rho,J)}{\rho^2}d\rho=0.$$
Then \ref{1} has the form
$$\frac{\partial S}{\partial t}+u\frac{\partial S}{\partial x}=0.\tag{1prm}$$
On the left-hand sides of \ref{1prm} and \ref{2} there stand the derivatives $dS/dt$, $dp/dt$, $du/dt$, taken in the directions
$$\frac{dx}{dt}=u\tag{3}$$
and
$$\frac{dx}{dt}=u\pm c,\tag{4}$$
the so-called characteristics. The system \ref{1}, \ref{2} has three families of real characteristics. Along the characteristics \ref{3} the relation
$$dS=0$$
holds, and along the characteristic \ref{4} the relations
$$dp\pm\rho cdu=0\tag{5}$$
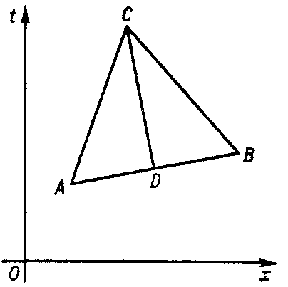
Figure: m063580a
hold. Through the point $A$ (see Fig.) there passes a characteristic \ref{4} on the side of increasing $t$,
$$\frac{x-x_A}{t-t_A}=u_A+c_A.$$
Through a point close to $A$ on the right, say $B$, there passes a characteristic \ref{4} of another family
$$\frac{x-x_B}{t-t_B}=u_B-c_B,$$
where $C$ is the point of intersection of the characteristics. When one replaces the differential relations \ref{5}, which hold along characteristics, by differences, one obtains the algebraic system
$$(p_C-p_A)+\rho_Ac_A(u_C-u_A)=0,$$
$$(p_C-p_B)-\rho_Bc_B(u_C-u_B)=0,$$
from which $p_C$ and $u_C$ can be determined. From $C$ one draws the characteristic \ref{3},
$$\frac{x-x_C}{t-t_C}=u_C,$$
up to the intersection with $AB$ at $D$. The value of the entropy $S$ at $D$ is determined by means of interpolation between the points $A$ and $B$ (here $S_C=S_D$). From the equations
$$p(\rho_C,J_C)=p_C,$$
$$S(\rho_C,J_C)=S_C$$
one can find the values of the intrinsic energy $J_C$ and the density $\rho_C$ at $C$. When the data at the two points $A$ and $D$ are known, one can find the solution at $C$ for large values of $t$. This procedure of computations is repeated for every pair of points. Then, by using new points $C$ instead of the original $A$ and $B$, one takes the next step in $t$. The calculation is made for the required values of $t$. However, since the equations of gas dynamics are non-linear, the calculation may come to a stop at a certain moment of time if the characteristics of one family touch each other or intersect.
The difference scheme thus described is of the first order of accuracy (an analogue of Euler's method of polygonal lines for solving ordinary differential equations). An increase in accuracy can be achieved by repetitions of the calculations, etc.
Using the method of characteristics one can solve stationary multi-dimensional problems in a domain of hyperbolicity (for gas dynamics — of supersonic flow). One can also determine the position of secondary shock waves at places where the characteristics of a single family intersect or touch. By the method of characteristics one can tackle only problems with a small number of discontinuities, since under an accumulation of singularities the computations become tedious. A computation by the method of characteristics consists of a number of elementary problems: the calculation of an interior point, of a point on the shock wave, or on a body around which the flow is taking place, etc.
One can construct numerical schemes for the method of characteristics, which make it possible to carry out the calculations in "layers" , the grid-characteristic method (see [2]).
References
| [1] | , An attempt at calculating plane and axially-symmetric supersonic flows of a gas by the method of characteristics , Moscow (1961) (In Russian) |
| [2] | K.M. Magomedov, A.S. Kholodov, "The constructions of difference schemes for hyperbolic equations based on characteristic relations" USSR Math. Math. Comp. , 9 : 2 (1969) pp. 158–176 Zh. Vyshch. Mat. i Mat. Fiz. , 9 : 2 (1969) pp. 373–386 |
Comments
The method of characteristics goes back to J. Massau (see [a2]).
References
| [a1] | W.F. Ames, "Numerical methods for partial differential equations" , Acad. Press (1977) MR0519123 Zbl 0577.65077 |
| [a2] | J. Massau, "Mémoire sur l'intégration graphique des équations aux derivées partielles" , F. Mayer-van Loo , Ghent (1899) MR0052203 Zbl 30.0312.01 |
Method of characteristics. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Method_of_characteristics&oldid=33484