Difference between revisions of "Helical line"
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| + | {{TEX|done}} | ||
A curve in space situated on the surface of a circular cylinder (a cylindrical helical line; see Fig. a) or a circular cone (a conical helical line; see Fig. b) which intersects all generators at the same angle. | A curve in space situated on the surface of a circular cylinder (a cylindrical helical line; see Fig. a) or a circular cone (a conical helical line; see Fig. b) which intersects all generators at the same angle. | ||
| Line 11: | Line 12: | ||
The parametric equations of a cylindrical helical line are | The parametric equations of a cylindrical helical line are | ||
| − | + | $$x=a\cos t,\quad y=a\sin t,\quad z=ht,$$ | |
| − | where | + | where $t$ is proportional to the arc length of the curve and $a$ is the radius of the cylinder. The parallel projection of a cylindrical helical line onto a plane parallel to the generators of the cylinder is a sinusoid. The curvature and the torsion of a cylindrical helical line are constant. The principal normals of a cylindrical helical line intersect the cylinder axis at a right angle. The length of a segment of a helical line between two of its successive points of intersection with the same generator is called the turn of the helical line, while the length of the corresponding segment on the generator is said to be the pace of the helical line. The parametric equations of a conical helical line are: |
| − | + | $$x=ce^{mt}\cos t,\quad y=ce^{mt}\sin t,\quad z=ce^{mt}\operatorname{cotan}\alpha,$$ | |
| − | where | + | where $t$ is the angular parameter on the basic circle for the cone, $\alpha$ is the angle between the axis of the cone and some generator, $m=\sin\alpha/\tan\phi$, and $\phi$ is the angle between the tangent to the helical line and the corresponding generator of the cone. The projection of the conical helical line parallel to the axis of the cone onto the plane perpendicular to the axis of the cone is a logarithmic spiral with pole in the projection of the apex of the cone. The ratio between the curvature and the torsion of a helical line remains constant at all points. |
| − | One distinguishes between right-handed and left-handed helical lines, i.e. as the value of the coordinate | + | One distinguishes between right-handed and left-handed helical lines, i.e. as the value of the coordinate $z$ increases, the rotation of the helical line around the axis is clockwise or counter-clockwise. A generalized helical line is a line on an arbitrary cylinder which intersects all generators of the cylinder at a constant angle. A helical line is a special case of a [[Curve of constant slope|curve of constant slope]]. |
====References==== | ====References==== | ||
Latest revision as of 15:42, 29 September 2014
A curve in space situated on the surface of a circular cylinder (a cylindrical helical line; see Fig. a) or a circular cone (a conical helical line; see Fig. b) which intersects all generators at the same angle.
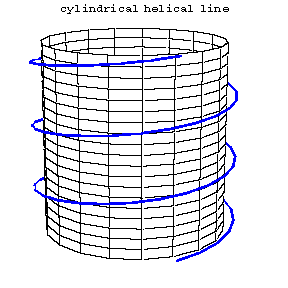
Figure: h046870a
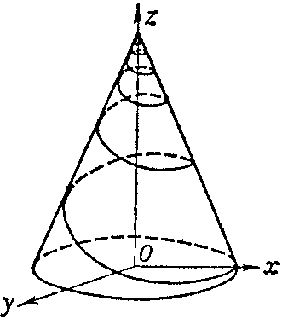
Figure: h046870b
The parametric equations of a cylindrical helical line are
$$x=a\cos t,\quad y=a\sin t,\quad z=ht,$$
where $t$ is proportional to the arc length of the curve and $a$ is the radius of the cylinder. The parallel projection of a cylindrical helical line onto a plane parallel to the generators of the cylinder is a sinusoid. The curvature and the torsion of a cylindrical helical line are constant. The principal normals of a cylindrical helical line intersect the cylinder axis at a right angle. The length of a segment of a helical line between two of its successive points of intersection with the same generator is called the turn of the helical line, while the length of the corresponding segment on the generator is said to be the pace of the helical line. The parametric equations of a conical helical line are:
$$x=ce^{mt}\cos t,\quad y=ce^{mt}\sin t,\quad z=ce^{mt}\operatorname{cotan}\alpha,$$
where $t$ is the angular parameter on the basic circle for the cone, $\alpha$ is the angle between the axis of the cone and some generator, $m=\sin\alpha/\tan\phi$, and $\phi$ is the angle between the tangent to the helical line and the corresponding generator of the cone. The projection of the conical helical line parallel to the axis of the cone onto the plane perpendicular to the axis of the cone is a logarithmic spiral with pole in the projection of the apex of the cone. The ratio between the curvature and the torsion of a helical line remains constant at all points.
One distinguishes between right-handed and left-handed helical lines, i.e. as the value of the coordinate $z$ increases, the rotation of the helical line around the axis is clockwise or counter-clockwise. A generalized helical line is a line on an arbitrary cylinder which intersects all generators of the cylinder at a constant angle. A helical line is a special case of a curve of constant slope.
References
| [1] | S.S. Byushgens, "Differential geometry" , Moscow-Leningrad (1940) (In Russian) |
| [2] | W. Blaschke, "Einführung in die Differentialgeometrie" , Springer (1950) |
Comments
A helical line is also called a helix.
References
| [a1] | M.P. Do Carmo, "Differential geometry of curves and surfaces" , Prentice-Hall (1976) pp. 26 |
| [a2] | M. Berger, B. Gostiaux, "Differential geometry: manifolds, curves, and surfaces" , Springer (1988) (Translated from French) |
| [a3] | K. Leichtweiss, "Einführung in die Differentialgeometrie" , Springer (1973) |
Helical line. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Helical_line&oldid=33441