Difference between revisions of "T-ideal"
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| + | {{TEX|done}} | ||
''of a free associative algebra'' | ''of a free associative algebra'' | ||
| − | A totally invariant ideal, that is, an ideal invariant under all endomorphisms. The set of all polynomial identities of an arbitrary variety of associative algebras over a field | + | A totally invariant ideal, that is, an ideal invariant under all endomorphisms. The set of all polynomial identities of an arbitrary variety of associative algebras over a field $F$ (cf. [[Associative rings and algebras|Associative rings and algebras]]) forms a $T$-ideal in the countably-generated free algebra $F[X]$, $X=\{x_1,\dots,x_k,\dots\}$. Thus, there exists a one-to-one correspondence between the $T$-ideals of $F[X]$ and the varieties of associative algebras over $F$. If $F$ has characteristic $0$, then for every $T$-ideal $T\subseteq F[X]$ there exists a natural number $n=n(T)$ such that certain powers of elements of $M_n(F)$ are elements of $T$, and only they, where $M_n(F)$ is the ideal of identities of the algebra $F_n$ of all $(n\times n)$-matrices over $F$. In this case a $T$-ideal can also be defined as a (two-sided) ideal that is closed under all differentiations of the free algebra. The quotient algebra $F[X]/T$ is a [[PI-algebra|PI-algebra]] with $T$ as set of polynomial identities. It is called the relatively free algebra (or generic algebra) with $T$-ideal of identities $T$ (and is a free algebra in the variety of algebras defined by the identities in $T$). The algebra $F[X]/T$ has no zero divisors if and only if $T=M_n(F)$ for some natural number $n$. Every $T$-ideal $T$ of a free associative algebra is primary. |
| − | The | + | The $T$-ideals of a free associative algebra on infinitely many generators over a field of characteristic zero form a free semi-group under the operation of multiplication of ideals. In this case a $T$-ideal can be defined as an ideal invariant under all automorphisms of the free algebra. |
| − | For the question as to whether every | + | For the question as to whether every $T$-ideal of $F[X]$ is the totally invariant closure of finitely many elements (Specht's problem) see also [[Variety of rings|Variety of rings]]. |
| − | + | $T$-ideals can be defined for non-associative algebras (Lie, alternative and others) by analogy with the associative case. | |
====References==== | ====References==== | ||
| Line 15: | Line 16: | ||
====Comments==== | ====Comments==== | ||
| − | A.R. Kemer has positively solved the Specht problem in the case of characteristic zero (see [[Variety of rings|Variety of rings]]). He has also introduced the notion of a | + | A.R. Kemer has positively solved the Specht problem in the case of characteristic zero (see [[Variety of rings|Variety of rings]]). He has also introduced the notion of a $T$-prime ideal, i.e. if $f[x_1,\dots,x_n]g[x_{n+1},\dots,x_m]\equiv0$ ($\bmod\,P$) for a $T$-ideal $P$, with different variables in $f$ and $g$, then either $f[x_1,\dots,x_n]\in P$ or $g[x_{n+1},\dots,x_m]\in P$. Similarly, for a $T$-nilpotent ideal. He has shown that for every $T$-ideal $I$ there exists a $T$-ideal $N(I)\supset I$ such that $N(I)/I$ is $T$-nilpotent and $N(I)$ is a finite product of $T$-prime ideals. |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A.R. Kemer, "Solution of the finite basis problem" ''Soviet Math. Dokl.'' , '''37''' (1988) pp. 60–64 ''Dokl. Akad. Nauk SSSR'' , '''298''' (1988) pp. 273–277</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A.R. Kemer, "Finite basis property of identities of associative algebras" ''Algebra and Logic'' , '''26''' (1987) pp. 362–397 ''Algebra i Logika'' , '''26''' (1987) pp. 597–641</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> E. Formanek, "The polynomial identities and invariants of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092020/t09202058.png" /> matrices" , Amer. Math. Soc. (1991)</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> A.R. Kemer, "Solution of the finite basis problem" ''Soviet Math. Dokl.'' , '''37''' (1988) pp. 60–64 ''Dokl. Akad. Nauk SSSR'' , '''298''' (1988) pp. 273–277</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A.R. Kemer, "Finite basis property of identities of associative algebras" ''Algebra and Logic'' , '''26''' (1987) pp. 362–397 ''Algebra i Logika'' , '''26''' (1987) pp. 597–641</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> E. Formanek, "The polynomial identities and invariants of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t092/t092020/t09202058.png" /> matrices" , Amer. Math. Soc. (1991)</TD></TR></table> | ||
Latest revision as of 08:33, 29 August 2014
of a free associative algebra
A totally invariant ideal, that is, an ideal invariant under all endomorphisms. The set of all polynomial identities of an arbitrary variety of associative algebras over a field $F$ (cf. Associative rings and algebras) forms a $T$-ideal in the countably-generated free algebra $F[X]$, $X=\{x_1,\dots,x_k,\dots\}$. Thus, there exists a one-to-one correspondence between the $T$-ideals of $F[X]$ and the varieties of associative algebras over $F$. If $F$ has characteristic $0$, then for every $T$-ideal $T\subseteq F[X]$ there exists a natural number $n=n(T)$ such that certain powers of elements of $M_n(F)$ are elements of $T$, and only they, where $M_n(F)$ is the ideal of identities of the algebra $F_n$ of all $(n\times n)$-matrices over $F$. In this case a $T$-ideal can also be defined as a (two-sided) ideal that is closed under all differentiations of the free algebra. The quotient algebra $F[X]/T$ is a PI-algebra with $T$ as set of polynomial identities. It is called the relatively free algebra (or generic algebra) with $T$-ideal of identities $T$ (and is a free algebra in the variety of algebras defined by the identities in $T$). The algebra $F[X]/T$ has no zero divisors if and only if $T=M_n(F)$ for some natural number $n$. Every $T$-ideal $T$ of a free associative algebra is primary.
The $T$-ideals of a free associative algebra on infinitely many generators over a field of characteristic zero form a free semi-group under the operation of multiplication of ideals. In this case a $T$-ideal can be defined as an ideal invariant under all automorphisms of the free algebra.
For the question as to whether every $T$-ideal of $F[X]$ is the totally invariant closure of finitely many elements (Specht's problem) see also Variety of rings.
$T$-ideals can be defined for non-associative algebras (Lie, alternative and others) by analogy with the associative case.
References
| [1] | C. Procesi, "Rings with polynomial identities" , M. Dekker (1973) |
| [2] | N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956) |
| [3] | I.N. Herstein, "Noncommutative rings" , Math. Assoc. Amer. (1968) |
| [4] | S. Amitsur, "The 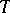 -ideals of the free ring" J. London Math. Soc. , 30 (1955) pp. 470–475 -ideals of the free ring" J. London Math. Soc. , 30 (1955) pp. 470–475 |
| [5] | W. Specht, "Gesetze in Ringen I" Math. Z. , 52 (1950) pp. 557–589 |
| [6] | G. Bergman, J. Lewin, "The semigroup of ideals of a fir is (usually) free" J. London Math. Soc. (2) , 11 : 1 (1975) pp. 21–31 |
Comments
A.R. Kemer has positively solved the Specht problem in the case of characteristic zero (see Variety of rings). He has also introduced the notion of a $T$-prime ideal, i.e. if $f[x_1,\dots,x_n]g[x_{n+1},\dots,x_m]\equiv0$ ($\bmod\,P$) for a $T$-ideal $P$, with different variables in $f$ and $g$, then either $f[x_1,\dots,x_n]\in P$ or $g[x_{n+1},\dots,x_m]\in P$. Similarly, for a $T$-nilpotent ideal. He has shown that for every $T$-ideal $I$ there exists a $T$-ideal $N(I)\supset I$ such that $N(I)/I$ is $T$-nilpotent and $N(I)$ is a finite product of $T$-prime ideals.
References
| [a1] | A.R. Kemer, "Solution of the finite basis problem" Soviet Math. Dokl. , 37 (1988) pp. 60–64 Dokl. Akad. Nauk SSSR , 298 (1988) pp. 273–277 |
| [a2] | A.R. Kemer, "Finite basis property of identities of associative algebras" Algebra and Logic , 26 (1987) pp. 362–397 Algebra i Logika , 26 (1987) pp. 597–641 |
| [a3] | E. Formanek, "The polynomial identities and invariants of 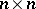 matrices" , Amer. Math. Soc. (1991) matrices" , Amer. Math. Soc. (1991) |
T-ideal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=T-ideal&oldid=33191