Difference between revisions of "Titchmarsh-Weyl m-function"
(more TeX) |
|||
| Line 15: | Line 15: | ||
$$ | $$ | ||
| − | Now consider a real boundary condition at < | + | Now consider a real boundary condition at $b'$, $a<b'<b$, of the form |
| − | + | $$\cos\beta x(b')+\sin\beta px'(b')=0,$$ | |
| − | and let | + | and let $\chi(x,\lambda)=\phi(x,\lambda)+\mathrm l(\lambda)\psi(x,\lambda)$ satisfy it. Then |
| − | + | $$\mathrm l(\lambda)=\frac{-(\cot\beta\phi(b',\lambda)+p\phi'(b',\lambda))}{\cot\beta\psi(b'(\lambda)+p\psi'(b',\lambda)}.$$ | |
| − | If | + | If $z=\cos\beta$, $\mathrm l$ is a [[Meromorphic function|meromorphic function]] in the complex $z$-plane; indeed, it is a bilinear transformation. As $\beta$ varies over real values $0\leq\beta\leq\pi$, $z$ varies over the real $z$-axis, and $\mathrm l$ describes a circle in the $z$-plane. |
| − | It can be shown that if | + | It can be shown that if $b'$ increases, the circles become nested. Hence there is at least one point inside all. For such a point $\mathrm l=m(\lambda)$, |
| − | < | + | $$\int\limits_a^b|\chi(x,\lambda)|^2w(x)dx<\infty.$$ |
| − | There exists at least one solution of | + | There exists at least one solution of $Ly=\lambda y$, which is square-integrable. |
| − | If the limit of the circles is a point, then | + | If the limit of the circles is a point, then $m(\lambda)$ is unique and only $\chi(x,\lambda)$ is square-integrable. This is the limit-point case. If the limit of the circles is itself a circle, then $m(\lambda)$ is not unique and all solutions of $Ly=\lambda y$ are square-integrable. This is the limit-circle case. |
Nonetheless, the differential operator | Nonetheless, the differential operator | ||
| − | + | $$Ly=\frac{-(py')'+qy}{w}$$ | |
whose domain satisfies | whose domain satisfies | ||
| − | + | $$\sin\alpha y(a)-\cos\alpha by'(a)=0,$$ | |
| − | + | $$\lim_{x\to b}[p(x)(y(x)\chi'(\lambda,x)-y'(x)\chi(x,\lambda)]=0,$$ | |
| − | where | + | where $\mathrm l=m$ on the limit circle or limit point, is a self-adjoint differential operator (cf. also [[Self-adjoint operator|Self-adjoint operator]]; [[Self-adjoint differential equation|Self-adjoint differential equation]]) on $L^2(a,b;w)$. |
| − | If the circle limit is a point, the second boundary condition (at | + | If the circle limit is a point, the second boundary condition (at $b$) is automatic. |
| − | The [[Spectral measure|spectral measure]] of | + | The [[Spectral measure|spectral measure]] of $L$ is given by |
| − | + | $$\rho(\lambda)-\rho(\mu)=\frac1\pi\lim_{\epsilon\to0}\int\limits_\mu^\lambda\operatorname{Im}(m(\nu+i\epsilon))d\nu.$$ | |
| − | The [[Spectral resolution|spectral resolution]] of arbitrary functions in | + | The [[Spectral resolution|spectral resolution]] of arbitrary functions in $L^2(a,b;w)$ is |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120120/t12012047.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t120/t120120/t12012047.png" /></td> </tr></table> | ||
| Line 57: | Line 57: | ||
where the limit is in the mean-square sense, and | where the limit is in the mean-square sense, and | ||
| − | + | $$g(\lambda)=\lim_{b'\to b}\int\limits_a^{b'}f(x)\psi(x,\lambda)dx.$$ | |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A.M. Krall, " | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A.M. Krall, "$M(\lambda)$ theory for singular Hamiltonian systems with one singular point" ''SIAM J. Math. Anal.'' , '''20''' (1989) pp. 644–700</TD></TR></table> |
Revision as of 16:35, 21 August 2014
A function arising in an attempt to properly determine which singular boundary-value problems are self-adjoint (cf. also Self-adjoint differential equation). Begin with a formally symmetric differential expression
$$ L y = \frac{-(p y')' + q y}{w} , $$
where $p\ne 0$, $q,w>0$ are measurable coefficients over $[a,b)$, and which is defined on a domain within $L^2(a,b;w)$. The Titchmarsh–Weyl $m$-function is defined as follows: For $\lambda = \mu + i \nu$, $\nu\ne 0$, let $\phi$ and $\psi$ be solutions of $L y = \lambda y$ satisfying
$$ \begin{aligned} \phi(a,\lambda) &= \sin\alpha, & \psi(a,\lambda) &= \cos\alpha, \\ p\phi'(a,\lambda) &= -\cos\alpha, & p\psi'(a,\lambda) &= \sin\alpha . \end{aligned} $$
Now consider a real boundary condition at $b'$, $a<b'<b$, of the form
$$\cos\beta x(b')+\sin\beta px'(b')=0,$$
and let $\chi(x,\lambda)=\phi(x,\lambda)+\mathrm l(\lambda)\psi(x,\lambda)$ satisfy it. Then
$$\mathrm l(\lambda)=\frac{-(\cot\beta\phi(b',\lambda)+p\phi'(b',\lambda))}{\cot\beta\psi(b'(\lambda)+p\psi'(b',\lambda)}.$$
If $z=\cos\beta$, $\mathrm l$ is a meromorphic function in the complex $z$-plane; indeed, it is a bilinear transformation. As $\beta$ varies over real values $0\leq\beta\leq\pi$, $z$ varies over the real $z$-axis, and $\mathrm l$ describes a circle in the $z$-plane.
It can be shown that if $b'$ increases, the circles become nested. Hence there is at least one point inside all. For such a point $\mathrm l=m(\lambda)$,
$$\int\limits_a^b|\chi(x,\lambda)|^2w(x)dx<\infty.$$
There exists at least one solution of $Ly=\lambda y$, which is square-integrable.
If the limit of the circles is a point, then $m(\lambda)$ is unique and only $\chi(x,\lambda)$ is square-integrable. This is the limit-point case. If the limit of the circles is itself a circle, then $m(\lambda)$ is not unique and all solutions of $Ly=\lambda y$ are square-integrable. This is the limit-circle case.
Nonetheless, the differential operator
$$Ly=\frac{-(py')'+qy}{w}$$
whose domain satisfies
$$\sin\alpha y(a)-\cos\alpha by'(a)=0,$$
$$\lim_{x\to b}[p(x)(y(x)\chi'(\lambda,x)-y'(x)\chi(x,\lambda)]=0,$$
where $\mathrm l=m$ on the limit circle or limit point, is a self-adjoint differential operator (cf. also Self-adjoint operator; Self-adjoint differential equation) on $L^2(a,b;w)$.
If the circle limit is a point, the second boundary condition (at $b$) is automatic.
The spectral measure of $L$ is given by
$$\rho(\lambda)-\rho(\mu)=\frac1\pi\lim_{\epsilon\to0}\int\limits_\mu^\lambda\operatorname{Im}(m(\nu+i\epsilon))d\nu.$$
The spectral resolution of arbitrary functions in $L^2(a,b;w)$ is
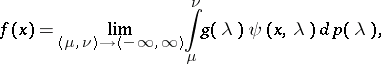 |
where the limit is in the mean-square sense, and
$$g(\lambda)=\lim_{b'\to b}\int\limits_a^{b'}f(x)\psi(x,\lambda)dx.$$
References
| [a1] | E.A. Coddington, N. Levinson, "Theory of ordinary differential equations" , McGraw-Hill (1955) |
| [a2] | A.M. Krall, "$M(\lambda)$ theory for singular Hamiltonian systems with one singular point" SIAM J. Math. Anal. , 20 (1989) pp. 644–700 |
Titchmarsh-Weyl m-function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Titchmarsh-Weyl_m-function&oldid=33047