Difference between revisions of "Range (of variation of a sample)"
From Encyclopedia of Mathematics
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| + | {{TEX|done}} | ||
The difference | The difference | ||
| − | + | $$w_n=x_\mathrm{max}-x_\mathrm{min}$$ | |
| − | between the largest | + | between the largest $x_\mathrm{max}=x_n$ and smallest $x_\mathrm{min}=x_1$ values in the ordered sample |
| − | + | $$(x_1,\ldots,x_n),\quad x_1\leq\ldots\leq x_n,$$ | |
| − | obtained by taking | + | obtained by taking $n$ independent measurements of the same random variable $X$. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077420/r0774207.png" /> be the distribution function of the random variable $X$. Then the probability distribution for the range is |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077420/r0774209.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/r/r077/r077420/r0774209.png" /></td> </tr></table> | ||
Revision as of 15:11, 1 August 2014
The difference
$$w_n=x_\mathrm{max}-x_\mathrm{min}$$
between the largest $x_\mathrm{max}=x_n$ and smallest $x_\mathrm{min}=x_1$ values in the ordered sample
$$(x_1,\ldots,x_n),\quad x_1\leq\ldots\leq x_n,$$
obtained by taking $n$ independent measurements of the same random variable $X$. Let 
be the distribution function of the random variable $X$. Then the probability distribution for the range is
 |
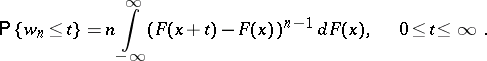References
| [1] | B.L. van der Waerden, "Mathematische Statistik" , Springer (1957) |
| [2] | L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) |
Comments
The range of variation of a sample is also called the sample range.
References
| [a1] | D.B. Owen, "Handbook of statistical tables" , Addison-Wesley (1962) |
How to Cite This Entry:
Range (of variation of a sample). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Range_(of_variation_of_a_sample)&oldid=32664
Range (of variation of a sample). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Range_(of_variation_of_a_sample)&oldid=32664
This article was adapted from an original article by T.Yu. Popova (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article