Difference between revisions of "Lituus"
From Encyclopedia of Mathematics
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| + | {{TEX|done}} | ||
A plane transcendental curve whose equation in polar coordinates is | A plane transcendental curve whose equation in polar coordinates is | ||
| − | + | $$\rho=\frac{a}{\sqrt\phi}.$$ | |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/l059750a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/l059750a.gif" /> | ||
| Line 7: | Line 8: | ||
Figure: l059750a | Figure: l059750a | ||
| − | To every value of | + | To every value of $\phi$ correspond two values of $\rho$, one positive and one negative. The curve consists of two branches, that both approach the pole asymptotically (see Fig.). The line $\phi=0,\phi=\pi$ is an asymptote at $\rho=\pm\infty$, and $(1/2,a\sqrt2)$ and $(-1/2,-a\sqrt2)$ are points of inflection. The lituus is related to the so-called algebraic [[Spirals|spirals]]. |
====References==== | ====References==== | ||
Revision as of 11:09, 26 July 2014
A plane transcendental curve whose equation in polar coordinates is
$$\rho=\frac{a}{\sqrt\phi}.$$
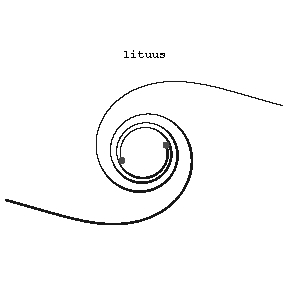
Figure: l059750a
To every value of $\phi$ correspond two values of $\rho$, one positive and one negative. The curve consists of two branches, that both approach the pole asymptotically (see Fig.). The line $\phi=0,\phi=\pi$ is an asymptote at $\rho=\pm\infty$, and $(1/2,a\sqrt2)$ and $(-1/2,-a\sqrt2)$ are points of inflection. The lituus is related to the so-called algebraic spirals.
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
Comments
References
| [a1] | K. Fladt, "Analytische Geometrie spezieller ebener Kurven" , Akad. Verlagsgesell. (1962) |
| [a2] | F. Gomes Teixeira, "Traité des courbes" , 1–3 , Chelsea, reprint (1971) |
How to Cite This Entry:
Lituus. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lituus&oldid=32535
Lituus. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lituus&oldid=32535
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article