Difference between revisions of "Archimedean spiral"
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| + | {{TEX|done}} | ||
A plane transcendental curve the equation of which in polar coordinates has the form: | A plane transcendental curve the equation of which in polar coordinates has the form: | ||
| − | + | $$\rho=a\phi.$$ | |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/a013150a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/a013150a.gif" /> | ||
| Line 7: | Line 8: | ||
Figure: a013150a | Figure: a013150a | ||
| − | It is described by a point | + | It is described by a point $M$ moving at a constant rate along a straight line $d$ that rotates around a point $O$ lying on that straight line. At the starting point of the motion, $M$ coincides with the centre of rotation $O$ of the straight line (see Fig.). The length of the arc between the points $M_1(\rho_1,\phi_1)$ and $M_2(\rho_2,\phi_2)$ is |
| − | + | $$l=\frac a2\left[\phi\sqrt{1+\phi^2}+\ln(\phi+\sqrt{1+\phi^2})\right]_{\phi_1}^{\phi_2}.$$ | |
| − | The area of the sector bounded by an arc of the Archimedean spiral and two radius vectors | + | The area of the sector bounded by an arc of the Archimedean spiral and two radius vectors $\rho_1$ and $\rho_2$, corresponding to angles $\phi_1$ and $\phi_2$, is |
| − | + | $$S=\frac{\rho_2^3-\rho_1^3}{a}.$$ | |
An Archimedean spiral is a so-called algebraic spiral (cf. [[Spirals|Spirals]]). The generalization of the Archimedean spiral is called a neoid, the equation of which in polar coordinates is | An Archimedean spiral is a so-called algebraic spiral (cf. [[Spirals|Spirals]]). The generalization of the Archimedean spiral is called a neoid, the equation of which in polar coordinates is | ||
| − | + | $$\rho=a\phi+l.$$ | |
The spiral was studied by Archimedes (3rd century B.C.) and was named after him. | The spiral was studied by Archimedes (3rd century B.C.) and was named after him. | ||
Revision as of 11:00, 26 July 2014
A plane transcendental curve the equation of which in polar coordinates has the form:
$$\rho=a\phi.$$
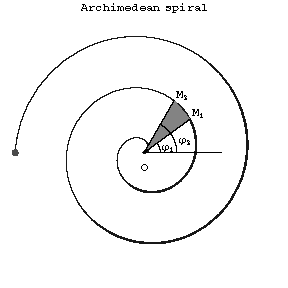
Figure: a013150a
It is described by a point $M$ moving at a constant rate along a straight line $d$ that rotates around a point $O$ lying on that straight line. At the starting point of the motion, $M$ coincides with the centre of rotation $O$ of the straight line (see Fig.). The length of the arc between the points $M_1(\rho_1,\phi_1)$ and $M_2(\rho_2,\phi_2)$ is
$$l=\frac a2\left[\phi\sqrt{1+\phi^2}+\ln(\phi+\sqrt{1+\phi^2})\right]_{\phi_1}^{\phi_2}.$$
The area of the sector bounded by an arc of the Archimedean spiral and two radius vectors $\rho_1$ and $\rho_2$, corresponding to angles $\phi_1$ and $\phi_2$, is
$$S=\frac{\rho_2^3-\rho_1^3}{a}.$$
An Archimedean spiral is a so-called algebraic spiral (cf. Spirals). The generalization of the Archimedean spiral is called a neoid, the equation of which in polar coordinates is
$$\rho=a\phi+l.$$
The spiral was studied by Archimedes (3rd century B.C.) and was named after him.
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
Comments
References
| [a1] | E.H. Lockwood, "A book of curves" , Cambridge Univ. Press (1961) |
Archimedean spiral. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Archimedean_spiral&oldid=32532