Difference between revisions of "Logarithmic paper"
From Encyclopedia of Mathematics
(Importing text file) |
(TeX) |
||
| Line 1: | Line 1: | ||
| + | {{TEX|done}} | ||
''double logarithmic paper'' | ''double logarithmic paper'' | ||
| − | A special form of ruled paper; it is usually made typographically (Fig. a) as follows: On each of the axes of a rectangular | + | A special form of ruled paper; it is usually made typographically (Fig. a) as follows: On each of the axes of a rectangular $(u,v)$-coordinate system one marks the decimal logarithms of numbers $u$ (on the horizontal axis) and $v$ (on the vertical axis) (cf. also [[Logarithm of a number|Logarithm of a number]]); then lines are drawn through the resulting points $(u,v)$ parallel to the axes. |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/l060620a.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/l060620a.gif" /> | ||
| Line 7: | Line 8: | ||
Figure: l060620a | Figure: l060620a | ||
| − | There is also semi-logarithmic paper (single logarithmic paper) (Fig. b): On one of the axes of a rectangular | + | There is also semi-logarithmic paper (single logarithmic paper) (Fig. b): On one of the axes of a rectangular $(u,v)$-coordinate system the values of numbers $u$ are marked, and on the other the decimal logarithms of numbers $v$. |
<img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/l060620b.gif" /> | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/l060620b.gif" /> | ||
| Line 13: | Line 14: | ||
Figure: l060620b | Figure: l060620b | ||
| − | Logarithmic paper and semi-logarithmic paper are used for drawing the graphs of functions which (in those coordinates) may take a simpler and more obvious form, and in many cases are straight lines. On logarithmic paper straight lines represent functions given by equations of the form | + | Logarithmic paper and semi-logarithmic paper are used for drawing the graphs of functions which (in those coordinates) may take a simpler and more obvious form, and in many cases are straight lines. On logarithmic paper straight lines represent functions given by equations of the form $v=au^b$, $u>0$, where $a>0$ and $b$ are constant coefficients; on semi-logarithmic paper straight lines represent functions given by equations of the form $v=ab^u$. |
Latest revision as of 20:38, 3 May 2014
double logarithmic paper
A special form of ruled paper; it is usually made typographically (Fig. a) as follows: On each of the axes of a rectangular $(u,v)$-coordinate system one marks the decimal logarithms of numbers $u$ (on the horizontal axis) and $v$ (on the vertical axis) (cf. also Logarithm of a number); then lines are drawn through the resulting points $(u,v)$ parallel to the axes.
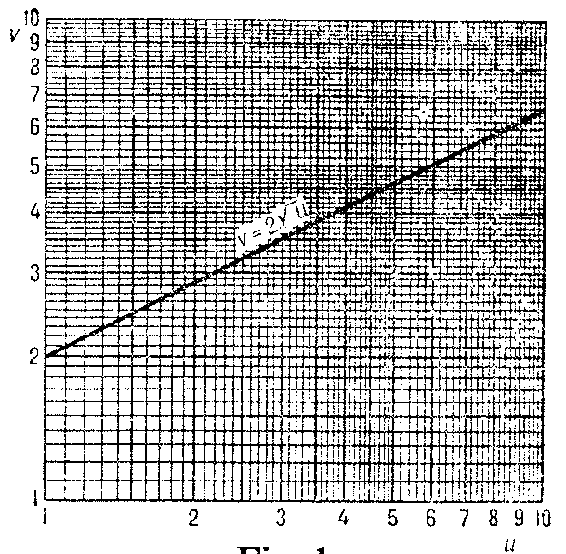
Figure: l060620a
There is also semi-logarithmic paper (single logarithmic paper) (Fig. b): On one of the axes of a rectangular $(u,v)$-coordinate system the values of numbers $u$ are marked, and on the other the decimal logarithms of numbers $v$.
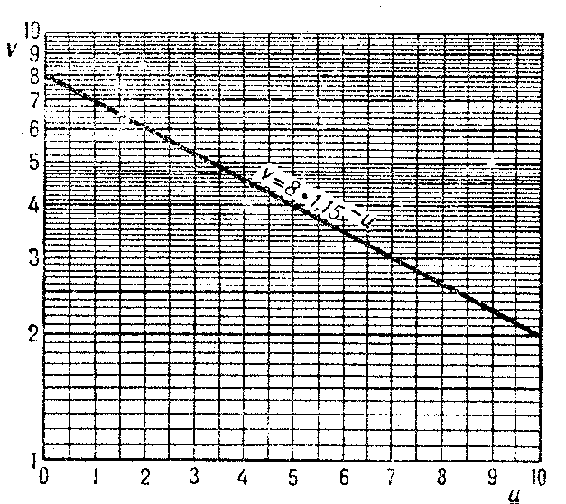
Figure: l060620b
Logarithmic paper and semi-logarithmic paper are used for drawing the graphs of functions which (in those coordinates) may take a simpler and more obvious form, and in many cases are straight lines. On logarithmic paper straight lines represent functions given by equations of the form $v=au^b$, $u>0$, where $a>0$ and $b$ are constant coefficients; on semi-logarithmic paper straight lines represent functions given by equations of the form $v=ab^u$.
How to Cite This Entry:
Logarithmic paper. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Logarithmic_paper&oldid=32138
Logarithmic paper. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Logarithmic_paper&oldid=32138
This article was adapted from an original article by BSE-3 (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article