Difference between revisions of "Quantum Turing machine"
m (Image added) |
|||
| Line 38: | Line 38: | ||
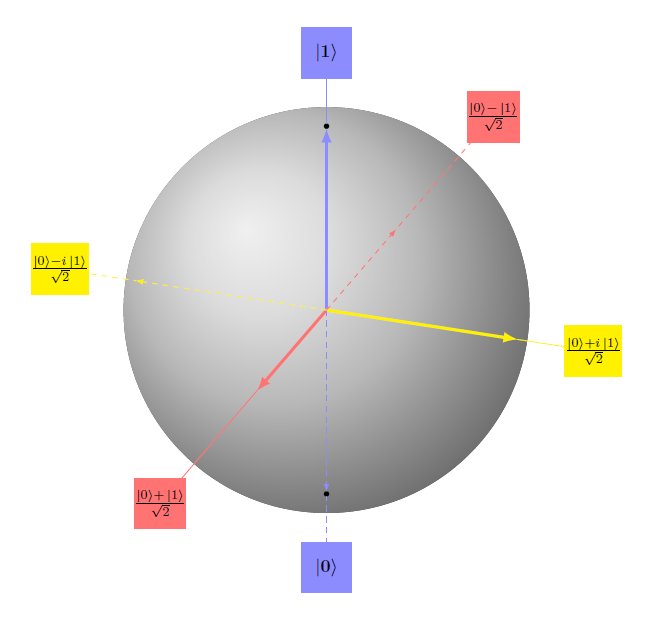
The situation described here is not identical with a random bit having values $\{0,1\}$ and probabilities $|\alpha|^2 $, $|\beta|^2$. Whereas a total of 4 different transformations can explain all possible transformations of a random bit, a Qubit can be transformed in infinitely many ways. The possible transformations applied on a Qubit can be represented by rotations of a so-called Bloch sphere. | The situation described here is not identical with a random bit having values $\{0,1\}$ and probabilities $|\alpha|^2 $, $|\beta|^2$. Whereas a total of 4 different transformations can explain all possible transformations of a random bit, a Qubit can be transformed in infinitely many ways. The possible transformations applied on a Qubit can be represented by rotations of a so-called Bloch sphere. | ||
| + | |||
| + | [[File:Bloch_sphere.png|center|Bloch Sphere]] | ||
===References=== | ===References=== | ||
Revision as of 17:16, 24 April 2014
2020 Mathematics Subject Classification: Primary: 68Q05 Secondary: 03D10 [MSN][ZBL]
The quantum Turing machine (QTM) is the quantum analogon of a Turing machine (TM). For many aspects, a close analogy to the classical counterpart exists. Though a quantum Turing machine can be defined more or less canonically, several conceptional problems associated with it and concerning the notion of 'quantum computation' exist and are still unsolved. Other properties of the quantum Turing machine like the question, whether universality does hold or not, are unknown as well.
Quantum Aspects of Computation
Church-Turing Thesis
The Church-Turing thesis defines an 'algorithm' as a description of a calculation. But is this the whole story? A calculation is not only a platonic object, usually it is intended to execute the actual calculation in one way or the other. Put in other words, the calculation should be realized physically. Then, the device executing the calculation has to be considered as physical system. A calculation is the execution of a physical experiment, and its result is provided by the observation of the experiment.
Today, many devices executing calculations are known. They are not limited to digital computers. Other types are e.g. analogous computers, soap-bubble based computers, the DNA-computing approach, and the Antikythera mechanism. This leads to the question, whether the restriction to classical models of computation like Turing machines is really adequate.
Church-Turing-Deutsch Thesis
The idea of the Turing machine dates back to the year 1936. At this time, the physical world seemed to be dominated by mechanical forces; correspondingly, the definition of a Turing machine is based on the ideas of classical mechanics. And though the physical realization of a Turing machine, the digital computer, actually uses quantum mechanics, its construction principles aims at the suppression of any effect associated with the quantum world. With ever-tighter package density, however, this is not achievable anymore in a perfect way. The effects of quantum theory may begin to have an influence on the outcome of the calculation.
Considered from another perspective, computations executed by humans are mental processes. In this way, the Church-Turing thesis is also a statement about the human mind. The Platonic world (including computations) is a mental construction. The brain, which is generating the Platonic world, is a physical system in turn; and at the microscopic level, this system has a quantum mechanical nature.
Consequently it seems to be questionable whether the Turing machine provides a 'natural' model of computation. Searching for alternatives and taking the quantum nature of the world into consideration, Feynman has the idea of quantum computation in 1982. As model executing such a quantum computation, he proposes the quantum Turing machine as quantum theoretical analogon to the Turing machine. Similar ideas were developed independently by Yuri Manin in 1980. Accordingly, David Deutsch generalized the Church-Turing thesis to the Church-Turing-Deutsch thesis in 1985, which states that every computation, which can be realized physically, can be executed using a quantum Turing machine.
Quantum Measurements
This section summarizes basic properties of quantum measurements. They are the necessary prerequisite for the discussion of quantum Turing machines. In order to simplify the following considerations, we will make two assumptions.
- The eigenspaces are not degenerated
- The operators associated with measurements have a discrete spectrum
These assumptions help us to concentrate on the foundations instead of technicalities.
Let us now consider a measurement executed by applying an observable $\hat O=|\psi_i \rangle\langle \psi_i |$ having an Eigenvalue $a_i$ with a corresponding Eigenvector $| \psi_i\rangle$. The probability $p$ of measuring the Eigenvalue $a_i$ in a state $| \psi\rangle=\sum_l \alpha_l | \psi_l\rangle \in\mathcal{H}$ is given by $p=|\langle \psi_i |\psi\rangle|^2= |\alpha_i|^2$. When measuring the Eigenvalue $a_i$, the original state $| \psi\rangle$ is changed to the corresponding Eigenvector $| \psi_i\rangle\in\mathcal{H}$ as new quantum state.
Quantum theory would not be probabilistical without measurements. The probabilistic nature could be explained as a result of an interaction between the measurement system and the quantum system, which leads to an entanglement of states. Consequently, the quantum system does not evolve independent from the outside world anymore, its future state is influenced by the measurement system.
Example: Qubits
A Qubit represents a quantum state $Q$ having 2 ground states $\{0,1\}$. Accordingly, $Q$ is given by $$ Q= \alpha | 0\rangle + \beta | 1\rangle.$$ This leads to a 2-dimensional Hilbert-space $\mathcal{H}\cong \mathbb{C}^2$. The probabilities of measuring the ground states are equal to $|\alpha|^2$ and $|\beta|^2$. It holds $ |\alpha|^2 + |\beta|^2 = 1 $, i.e. for example $$Q=\frac{1}{\sqrt{2}}| 0\rangle - \frac{1}{\sqrt{2}}| 1\rangle.$$
The situation described here is not identical with a random bit having values $\{0,1\}$ and probabilities $|\alpha|^2 $, $|\beta|^2$. Whereas a total of 4 different transformations can explain all possible transformations of a random bit, a Qubit can be transformed in infinitely many ways. The possible transformations applied on a Qubit can be represented by rotations of a so-called Bloch sphere.
References
| [A2005] | Scott Aaronson, "Quantum computing, postselection, and probabilistic polynomial-time", Proceedings of the Royal Society A461(2005)3473-3482 |
| [A2013] | Scott Aaronson, "The Ghost in the Quantum Turing Machine", arXiv:1306.0159v2 [quant-ph] |
| [BC2006] | D.P. Bovet, P. Crescenzi, "Introduction to the theory of complexity", Lecture Notes, unpublished 2006 |
| [CC2010] | Goong Chen, David A. Church, Berthold-Georg Englert, Carsten Henkel, Bernd Rohwedder, Marlan O. Scully, M. Suhail Zubairy, "Quantum Computing Devices: Principles, Designs, and Analysis", CRC Press 2010 |
| [D1985] | David Deutsch, "Quantum theory, the Church-Turing principle and the universal quantum computer", Proceedings of the Royal Society of London A400(1985)97-117 |
| [F2003] | Lance Fortnow, "One Complexity Theorist's View of Quantum Computing", Theoretical Computer Science 292(3)(2003)597-610 |
| [F2007] | Willem Fouché, Johannes Heidema, Glyn Jones, Petrus H. Potgieter, "Deutsch's Universal Quantum Turing Machine (Revisited)", arXiv:0701108v1 [quant-ph] |
| [H1997] | Mika Hirvensalo, "On Quantum Computation", Licentiate's thesis, University of Turku 1997 |
| [M1980] | Yuri Manin, "Vychislimoe i nevychislimoe", Sov.Radio. 1980 |
| [MN1994] | Takashi Mihara, Tetsuro Nishino, "On a Method of Solving NP-Complete Problems in Polynomial Time Using the Quantum Turing Machine", in Maruoka, Akira (editor), "Computational complexity theory", Proceedings of a symposium held at Kyoto 1994, in RIMS Kokyuroku 871(1994)30-36 |
| [M2012] | Jaroslaw Miszczak, "High-Level Structures for Quantum Computing", Morgan & Claypool Publishers 2012 |
| [MO2002] | Takayuki Miyadera, Masanori Ohya, "Designing Quantum Turing Machine is uncomputable", in Proceeedings of the Erato Workshop on Quantum Information Science 2002 |
| [MO2005] | Takayuki Miyadera, Masanori Ohya, "On Halting Process of Quantum Turing Machine", Open Systems and Information Dynamics, 12(3)(2005)261-265 |
| [M2007] | Markus Müller, "Quantum Kolmogorov Complexity and the Quantum Turing Machine", PhD Thesis, Technischen Universität Berlin 2007 |
| [ON2000] | Masanao Ozawa, Harumichi Nishimura, "Local Transition Functions of Quantum Turing Machines", Theoret. Informatics and Appl. 34(2000)379-402 |
| [P2011] | Simon Perdrix, "Partial Observation of Quantum Turing Machine and Weaker Well-Formedness Condition", Electronic Notes in Theoretical Computer Science 270, Issue 1, (2011) pp. 99-111, also in B. Coecke, I. Mackie, P. Panangaden, P. Selinger (editors), Proceedings of the Joint 5th International Workshop on Quantum Physics and Logic and 4th Workshop on Developments in Computational Models QPL/DCM 2008 |
| [P2006] | P. Prashant, "The Church-Turing-Deutsch Principle in Quantum Computation", in Hamid R. Arabnia, Mark Murgin (Eds.), Proceedings of the 2006 International Conference on Foundations of Computer Science, Las Vegas 2006, CSREA Press 2006, pp. 141-148 |
| [S2000] | A. Stern, "Quantum Theoretic Machines: What is thought from the point of view of Physics?", Elsevier 2000 |
| [Y1993] | Andrew Yao, "Quantum circuit complexity", Proceedings of the 34th Annual Symposium on Foundations of Computer Science, 1993, pp. 352-361 |
Quantum Turing machine. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Quantum_Turing_machine&oldid=31915