Difference between revisions of "AF-algebra"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
m (starting Texify) |
||
| Line 1: | Line 1: | ||
| − | + | == Approximately Finite-dimensional algebra. == | |
| − | AF-algebras form a class of | + | AF-algebras form a class of $C^*$-algebras that, on the one hand, admits an elementary construction, yet, on the other hand, exhibits a rich structure and provide examples of exotic phenomena. A (separable) [[C*-algebra|$C^*$-algebra]] $A$ is said to be an ''AF-algebra'' if one of the following two (not obviously) equivalent conditions is satisfied (see [[#References|[a1]]], [[#References|[a2]]] or [[#References|[a6]]]): |
| − | + | # for every finite subset $\{a_1,\dots,a_n\}$ of $A$ and for every $\epsilon>0$ there exists a finite-dimensional sub-$C^*$-algebra $B$ of $A$ and a subset $\{b_1,\dots,b_n\}$ o f$B$ with $\|a_j-b_j\|<\epsilon$ for all $j=1,\dots,n$; | |
| + | # there exists an increasing sequence $A_1\subseteq A_2\subseteq\dots$ of finite-dimensional sub-$C^*$-algebras of $A$ such that the union $\bigcup_{j=1}^\infty A_j$ is norm-dense in $A$. | ||
| − | + | ==Bratteli diagrams. == | |
| − | |||
| − | ==Bratteli diagrams.== | ||
It follows from (an analogue of) Wedderburn's theorem (cf. [[Wedderburn–Artin theorem|Wedderburn–Artin theorem]]), that every finite-dimensional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110420/a11042019.png" />-algebra is isomorphic to the direct sum of full matrix algebras over the field of complex numbers. Property ii) says that each AF-algebra is the [[Inductive limit|inductive limit]] of a sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110420/a11042020.png" /> of finite-dimensional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110420/a11042021.png" />-algebras, where the connecting mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110420/a11042022.png" /> are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110420/a11042023.png" />-preserving homomorphisms. If two such sequences <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110420/a11042024.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110420/a11042025.png" /> define isomorphic AF-algebras, then already the algebraic inductive limits of the two sequences are isomorphic (as algebras over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110420/a11042026.png" />). | It follows from (an analogue of) Wedderburn's theorem (cf. [[Wedderburn–Artin theorem|Wedderburn–Artin theorem]]), that every finite-dimensional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110420/a11042019.png" />-algebra is isomorphic to the direct sum of full matrix algebras over the field of complex numbers. Property ii) says that each AF-algebra is the [[Inductive limit|inductive limit]] of a sequence <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110420/a11042020.png" /> of finite-dimensional <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110420/a11042021.png" />-algebras, where the connecting mappings <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110420/a11042022.png" /> are <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110420/a11042023.png" />-preserving homomorphisms. If two such sequences <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110420/a11042024.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110420/a11042025.png" /> define isomorphic AF-algebras, then already the algebraic inductive limits of the two sequences are isomorphic (as algebras over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a110/a110420/a11042026.png" />). | ||
Revision as of 18:38, 19 April 2014
Approximately Finite-dimensional algebra.
AF-algebras form a class of $C^*$-algebras that, on the one hand, admits an elementary construction, yet, on the other hand, exhibits a rich structure and provide examples of exotic phenomena. A (separable) $C^*$-algebra $A$ is said to be an AF-algebra if one of the following two (not obviously) equivalent conditions is satisfied (see [a1], [a2] or [a6]):
- for every finite subset $\{a_1,\dots,a_n\}$ of $A$ and for every $\epsilon>0$ there exists a finite-dimensional sub-$C^*$-algebra $B$ of $A$ and a subset $\{b_1,\dots,b_n\}$ o f$B$ with $\|a_j-b_j\|<\epsilon$ for all $j=1,\dots,n$;
- there exists an increasing sequence $A_1\subseteq A_2\subseteq\dots$ of finite-dimensional sub-$C^*$-algebras of $A$ such that the union $\bigcup_{j=1}^\infty A_j$ is norm-dense in $A$.
Bratteli diagrams.
It follows from (an analogue of) Wedderburn's theorem (cf. Wedderburn–Artin theorem), that every finite-dimensional 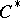 -algebra is isomorphic to the direct sum of full matrix algebras over the field of complex numbers. Property ii) says that each AF-algebra is the inductive limit of a sequence
-algebra is isomorphic to the direct sum of full matrix algebras over the field of complex numbers. Property ii) says that each AF-algebra is the inductive limit of a sequence 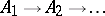 of finite-dimensional
of finite-dimensional 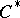 -algebras, where the connecting mappings
-algebras, where the connecting mappings 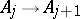 are
are 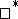 -preserving homomorphisms. If two such sequences
-preserving homomorphisms. If two such sequences 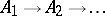 and
and 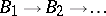 define isomorphic AF-algebras, then already the algebraic inductive limits of the two sequences are isomorphic (as algebras over
define isomorphic AF-algebras, then already the algebraic inductive limits of the two sequences are isomorphic (as algebras over 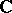 ).
).
All essential information of a sequence 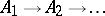 of finite-dimensional
of finite-dimensional 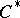 -algebras with connecting mappings can be expressed in a so-called Bratteli diagram. The Bratteli diagram is a graph, divided into rows, whose vertices in the
-algebras with connecting mappings can be expressed in a so-called Bratteli diagram. The Bratteli diagram is a graph, divided into rows, whose vertices in the 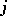 th row correspond to the direct summands of
th row correspond to the direct summands of 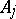 isomorphic to a full matrix algebra, and where the edges between the
isomorphic to a full matrix algebra, and where the edges between the 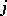 th and the
th and the 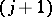 st row describe the connecting mapping
st row describe the connecting mapping 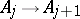 . By the facts mentioned above, the construction and also the classification of AF-algebras can be reduced to a purely combinatorial problem phrased in terms of Bratteli diagrams. (See [a2].)
. By the facts mentioned above, the construction and also the classification of AF-algebras can be reduced to a purely combinatorial problem phrased in terms of Bratteli diagrams. (See [a2].)
UHF-algebras.
AF-algebras that are inductive limits of single full matrix algebras with unit-preserving connecting mappings are called UHF-algebras (uniformly hyper-finite algebras) or Glimm algebras. A UHF-algebra is therefore an inductive limit of a sequence 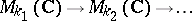 , where, necessarily, each
, where, necessarily, each 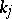 divides
divides 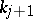 . Setting
. Setting 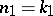 and
and 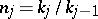 for
for 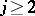 , this UHF-algebra can alternatively be described as the infinite tensor product
, this UHF-algebra can alternatively be described as the infinite tensor product 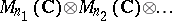 . (See [a1].)
. (See [a1].)
The UHF-algebra with 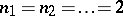 is called the CAR-algebra; it is generated by a family of operators
is called the CAR-algebra; it is generated by a family of operators 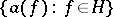 , where
, where 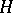 is some separable infinite-dimensional Hilbert space and
is some separable infinite-dimensional Hilbert space and  is linear and satisfies the canonical anti-commutation relations (cf. also Commutation and anti-commutation relationships, representation of):
is linear and satisfies the canonical anti-commutation relations (cf. also Commutation and anti-commutation relationships, representation of):
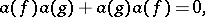 |
 |
(See [a7].)
 -theory and classification.
-theory and classification.
By the  -theory for
-theory for 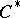 -algebras, one can associate a triple
-algebras, one can associate a triple 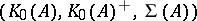 to each
to each 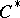 -algebra
-algebra 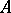 .
. 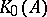 is the countable Abelian group of formal differences of equivalence classes of projections in matrix algebras over
is the countable Abelian group of formal differences of equivalence classes of projections in matrix algebras over 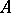 , and
, and 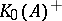 and
and 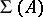 are the subsets of those elements in
are the subsets of those elements in 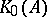 that are represented by projections in some matrix algebra over
that are represented by projections in some matrix algebra over 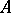 , respectively, by projections in
, respectively, by projections in 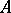 itself. The
itself. The 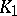 -group of an AF-algebra is always zero.
-group of an AF-algebra is always zero.
The classification theorem for AF-algebras says that two AF-algebras 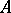 and
and 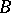 are
are 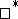 -isomorphic if and only if the triples
-isomorphic if and only if the triples 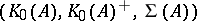 and
and 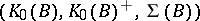 are isomorphic, i.e., if and only if there exists a group isomorphism
are isomorphic, i.e., if and only if there exists a group isomorphism 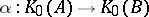 such that
such that 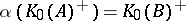 and
and 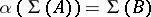 . If this is the case, then there exists an isomorphism
. If this is the case, then there exists an isomorphism 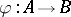 such that
such that 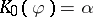 . Moreover, any homomorphism
. Moreover, any homomorphism 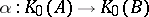 such that
such that 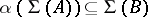 is induced by a
is induced by a 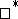 -homomorphism
-homomorphism 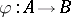 , and if
, and if 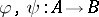 are two
are two 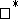 -homomorphisms, then
-homomorphisms, then 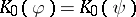 if and only if
if and only if 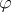 and
and 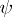 are homotopic (through a continuous path of
are homotopic (through a continuous path of 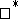 -homomorphisms from
-homomorphisms from 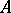 to
to 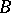 ).
).
An ordered Abelian group 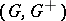 is said to have the Riesz interpolation property if whenever
is said to have the Riesz interpolation property if whenever 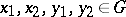 with
with 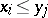 , there exists a
, there exists a 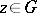 such that
such that 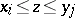 .
. 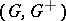 is called unperforated if
is called unperforated if 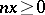 , for some integer
, for some integer 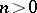 and some
and some 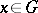 , implies that
, implies that 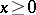 . The Effros–Handelman–Shen theorem says that a countable ordered Abelian group
. The Effros–Handelman–Shen theorem says that a countable ordered Abelian group 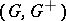 is the
is the 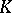 -theory of some AF-algebra if and only if it has the Riesz interpolation property and is unperforated. (See [a3], [a5], [a8], and [a6].)
-theory of some AF-algebra if and only if it has the Riesz interpolation property and is unperforated. (See [a3], [a5], [a8], and [a6].)
A conjecture belonging to the Elliott classification program asserts that a 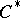 -algebra is an AF-algebra if it looks like an AF-algebra! More precisely, suppose that
-algebra is an AF-algebra if it looks like an AF-algebra! More precisely, suppose that 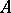 is a separable, nuclear
is a separable, nuclear 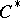 -algebra which has stable rank one and real rank zero, and suppose that
-algebra which has stable rank one and real rank zero, and suppose that 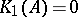 and that
and that 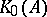 is unperforated (
is unperforated (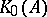 must necessarily have the Riesz interpolation property when
must necessarily have the Riesz interpolation property when 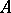 is assumed to be of real rank zero). Does it follow that
is assumed to be of real rank zero). Does it follow that 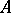 is an AF-algebra? This conjecture has been confirmed in some specific non-trivial cases. (See [a9].)
is an AF-algebra? This conjecture has been confirmed in some specific non-trivial cases. (See [a9].)
Traces and ideals.
The 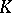 -theory of an AF-algebra not only serves as a classifying invariant, it also explicitly reveals some of the structure of the algebra, for example its traces and its ideal structure. Recall that a (positive) trace on a
-theory of an AF-algebra not only serves as a classifying invariant, it also explicitly reveals some of the structure of the algebra, for example its traces and its ideal structure. Recall that a (positive) trace on a 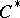 -algebra
-algebra 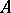 is a (positive) linear mapping
is a (positive) linear mapping 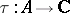 satisfying the trace property:
satisfying the trace property: 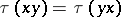 for all
for all 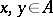 . An "ideal" means a closed two-sided ideal.
. An "ideal" means a closed two-sided ideal.
A state 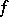 on an ordered Abelian group
on an ordered Abelian group 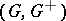 is a group homomorphism
is a group homomorphism 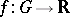 satisfying
satisfying 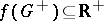 . An order ideal
. An order ideal 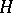 of
of 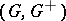 is a subgroup of
is a subgroup of 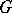 with the property that
with the property that 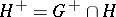 generates
generates 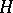 , and if
, and if 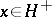 ,
, 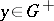 , and
, and 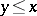 , then
, then 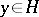 . A trace
. A trace  on
on 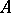 induces a state on
induces a state on 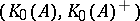 by
by
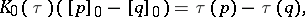 |
where 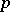 ,
, 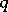 are projections in
are projections in 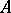 (or in a matrix algebra over
(or in a matrix algebra over 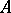 ); and given an ideal
); and given an ideal  in
in 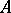 , the image
, the image 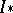 of the induced mapping
of the induced mapping 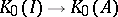 (which happens to be injective, when
(which happens to be injective, when 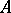 is an AF-algebra) is an order ideal of
is an AF-algebra) is an order ideal of 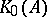 . For AF-algebras, the mappings
. For AF-algebras, the mappings  and
and 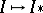 are bijections. In particular, if
are bijections. In particular, if  is simple as an ordered group, then
is simple as an ordered group, then 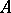 must be simple.
must be simple.
If a 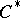 -algebra
-algebra 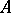 has a unit, then the set of tracial states (i.e., positive traces that take the value
has a unit, then the set of tracial states (i.e., positive traces that take the value 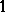 on the unit) is a Choquet simplex. Using the characterizations above, one can, for each metrizable Choquet simplex, find a simple unital AF-algebra whose trace simplex is affinely homeomorphic to the given Choquet simplex. Hence, for example, simple unital
on the unit) is a Choquet simplex. Using the characterizations above, one can, for each metrizable Choquet simplex, find a simple unital AF-algebra whose trace simplex is affinely homeomorphic to the given Choquet simplex. Hence, for example, simple unital 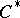 -algebras can have more than one trace. (See [a3] and [a5].)
-algebras can have more than one trace. (See [a3] and [a5].)
Embeddings into AF-algebras.
One particularly interesting, and still not fully investigated, application of AF-algebras is to find for a 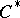 -algebra
-algebra 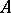 an AF-algebra
an AF-algebra 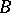 and an embedding
and an embedding 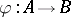 which induces an interesting (say injective) mapping
which induces an interesting (say injective) mapping 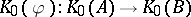 . Since
. Since 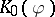 is positive, the positive cone
is positive, the positive cone 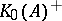 of
of 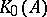 must be contained in the pre-image of
must be contained in the pre-image of 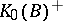 . For example, the order structure of the
. For example, the order structure of the 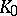 -group of the irrational rotation
-group of the irrational rotation 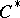 -algebra
-algebra 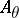 was determined by embedding
was determined by embedding 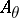 into an AF-algebra
into an AF-algebra 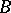 with
with 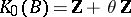 (as an ordered group). As a corollary to this, it was proved that
(as an ordered group). As a corollary to this, it was proved that 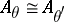 if and only if
if and only if  or
or 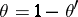 . (See [a4].)
. (See [a4].)
Along another interesting avenue there have been produced embeddings of 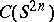 into appropriate AF-algebras inducing injective
into appropriate AF-algebras inducing injective 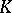 -theory mappings. This suggests that the "cohomological dimension" of these AF-algebras should be at least
-theory mappings. This suggests that the "cohomological dimension" of these AF-algebras should be at least 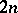 .
.
References
| [a1] | J. Glimm, "On a certain class of operator algebras" Trans. Amer. Math. Soc. , 95 (1960) pp. 318–340 MR0112057 Zbl 0094.09701 |
| [a2] | O. Bratteli, "Inductive limits of finite-dimensional 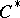 -algebras" Trans. Amer. Math. Soc. , 171 (1972) pp. 195–234 MR312282 -algebras" Trans. Amer. Math. Soc. , 171 (1972) pp. 195–234 MR312282 |
| [a3] | G.A. Elliott, "On the classification of inductive limits of sequences of semisimple finite-dimensional algebras" J. Algebra , 38 (1976) pp. 29–44 MR0397420 Zbl 0323.46063 |
| [a4] | M. Pimsner, D. Voiculescu, "Imbedding the irrational rotation algebras into AF-algebras" J. Operator Th. , 4 (1980) pp. 201–210 MR595412 |
| [a5] | E. Effros, D. Handelman, C.-L. Shen, "Dimension groups and their affine representations" Amer. J. Math. , 102 (1980) pp. 385–407 MR0564479 Zbl 0457.46047 |
| [a6] | E. Effros, "Dimensions and 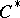 -algebras" , CBMS Regional Conf. Ser. Math. , 46 , Amer. Math. Soc. (1981) MR0623762 -algebras" , CBMS Regional Conf. Ser. Math. , 46 , Amer. Math. Soc. (1981) MR0623762 |
| [a7] | O. Bratteli, D.W. Robinson, "Operator algebras and quantum statistical mechanics" , II , Springer (1981) MR0611508 Zbl 0463.46052 |
| [a8] | B. Blackadar, "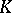 -theory for operator algebras" , MSRI publication , 5 , Springer (1986) MR0859867 Zbl 0597.46072 -theory for operator algebras" , MSRI publication , 5 , Springer (1986) MR0859867 Zbl 0597.46072 |
| [a9] | G.A. Elliott, "The classification problem for amenable 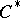 -algebras" , Proc. Internat. Congress Mathem. (Zürich, 1994) , Birkhäuser (1995) pp. 922–932 -algebras" , Proc. Internat. Congress Mathem. (Zürich, 1994) , Birkhäuser (1995) pp. 922–932 |
AF-algebra. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=AF-algebra&oldid=31881