|
|
| Line 1: |
Line 1: |
| − | ''of degree <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012030/a0120302.png" />'' | + | {{TEX|done}} |
| | + | ''of degree $n$'' |
| | | | |
| − | The subgroup <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012030/a0120303.png" /> of the [[Symmetric group|symmetric group]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012030/a0120304.png" /> consisting of all even permutations. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012030/a0120305.png" /> is a normal subgroup in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012030/a0120306.png" /> of index 2 and order <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012030/a0120307.png" />. The permutations of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012030/a0120308.png" />, considered as permutations of the indices of variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012030/a0120309.png" />, leave the alternating polynomial <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012030/a01203010.png" /> invariant, hence the term "alternating group" . The group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012030/a01203011.png" /> may also be defined for infinite cardinal numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012030/a01203012.png" />, as the subgroup of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012030/a01203013.png" /> consisting of all even permutations. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012030/a01203014.png" />, the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012030/a01203015.png" /> is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012030/a01203016.png" />-fold transitive. For any <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012030/a01203017.png" />, finite or infinite, except <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/a/a012/a012030/a01203018.png" />, this group is simple; this fact plays an important role in the theory of solvability of algebraic equations by radicals. | + | The subgroup $A_n$ of the [[Symmetric group|symmetric group]] $S_n$ consisting of all even permutations. $A_n$ is a normal subgroup in $S_n$ of index 2 and order $n!/2$. The permutations of $A_n$, considered as permutations of the indices of variables $x_1,\ldots,x_n$, leave the alternating polynomial $\prod(x_i-x_j)$ invariant, hence the term "alternating group" . The group $A_m$ may also be defined for infinite cardinal numbers $m$, as the subgroup of $S_n$ consisting of all even permutations. If $n>3$, the group $A_n$ is $(n-2)$-fold transitive. For any $n$, finite or infinite, except $n=4$, this group is simple; this fact plays an important role in the theory of solvability of algebraic equations by radicals. |
| | | | |
| | ====References==== | | ====References==== |
Revision as of 19:25, 17 April 2014
of degree $n$
The subgroup $A_n$ of the symmetric group $S_n$ consisting of all even permutations. $A_n$ is a normal subgroup in $S_n$ of index 2 and order $n!/2$. The permutations of $A_n$, considered as permutations of the indices of variables $x_1,\ldots,x_n$, leave the alternating polynomial $\prod(x_i-x_j)$ invariant, hence the term "alternating group" . The group $A_m$ may also be defined for infinite cardinal numbers $m$, as the subgroup of $S_n$ consisting of all even permutations. If $n>3$, the group $A_n$ is $(n-2)$-fold transitive. For any $n$, finite or infinite, except $n=4$, this group is simple; this fact plays an important role in the theory of solvability of algebraic equations by radicals.
References
| [1] | M. Hall, "Group theory" , Macmillan (1959) |
Note that 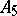 is the non-Abelian simple group of smallest possible order.
is the non-Abelian simple group of smallest possible order.
How to Cite This Entry:
Alternating group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Alternating_group&oldid=31834
This article was adapted from an original article by N.N. Vil'yams (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098.
See original article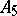 is the non-Abelian simple group of smallest possible order.
is the non-Abelian simple group of smallest possible order.