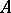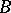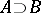Difference between revisions of "Implication"
From Encyclopedia of Mathematics
(Importing text file) |
(TeX; table) |
||
| Line 1: | Line 1: | ||
| − | The logical operation corresponding to the formation of the expression "if A, then B" from two expressions | + | {{TEX|done}} |
| + | The logical operation corresponding to the formation of the expression "if A, then B" from two expressions $A$ and $B$. In formal languages, implication is most often denoted by one of the symbols $\supset$, $\rightarrow$ or $\Rightarrow$. The expression $A$ is called the premise of $A\supset B$, while the expression $B$ is called the consequence. The precise meaning of the expression $A\supset B$ differs in the classical, constructive and other approaches to the semantics of the language. In languages with classical semantics, the use of implication is in accordance with the following [[Truth table|truth table]]:<table border="0" cellpadding="0" cellspacing="0" style="background-color:black;"> <tr><td> <table border="0" cellspacing="1" cellpadding="4" style="background-color:black;"> <tbody> <tr> <td colname="1" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050280/i05028010.png" /></td> <td colname="2" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050280/i05028011.png" /></td> <td colname="3" style="background-color:white;" colspan="1"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/i/i050/i050280/i05028012.png" /></td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">T</td> <td colname="2" style="background-color:white;" colspan="1">T</td> <td colname="3" style="background-color:white;" colspan="1">T</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">T</td> <td colname="2" style="background-color:white;" colspan="1">F</td> <td colname="3" style="background-color:white;" colspan="1">F</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">F</td> <td colname="2" style="background-color:white;" colspan="1">T</td> <td colname="3" style="background-color:white;" colspan="1">T</td> </tr> <tr> <td colname="1" style="background-color:white;" colspan="1">F</td> <td colname="2" style="background-color:white;" colspan="1">F</td> <td colname="3" style="background-color:white;" colspan="1">T</td> </tr> </tbody> </table> | ||
</td></tr> </table> | </td></tr> </table> | ||
Revision as of 10:24, 13 April 2014
The logical operation corresponding to the formation of the expression "if A, then B" from two expressions $A$ and $B$. In formal languages, implication is most often denoted by one of the symbols $\supset$, $\rightarrow$ or $\Rightarrow$. The expression $A$ is called the premise of $A\supset B$, while the expression $B$ is called the consequence. The precise meaning of the expression $A\supset B$ differs in the classical, constructive and other approaches to the semantics of the language. In languages with classical semantics, the use of implication is in accordance with the following truth table:
<tbody> </tbody>
|
Implication as understood in the above sense is called material implication.
Comments
References
| [a1] | J.L. Bell, M. Machover, "A course in mathematical logic" , North-Holland (1977) |
How to Cite This Entry:
Implication. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Implication&oldid=31670
Implication. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Implication&oldid=31670
This article was adapted from an original article by V.E. Plisko (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article