Difference between revisions of "Zero"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
(TeX) |
||
| Line 1: | Line 1: | ||
| − | A (real or complex) number having the property that any number does not change if zero is added to it. It is denoted by the symbol | + | A (real or complex) number having the property that any number does not change if zero is added to it. It is denoted by the symbol $0$. The product of any number with zero is zero: |
| + | $$0\cdot a = a \cdot 0 = 0 .$$ | ||
| − | + | If the product of two numbers is zero, then one of them is zero (that is, $a\cdot b = 0$ implies $a=0$ or $b=0$). Division by zero is not defined. A direct generalization of this concept is that of the zero of an Abelian group. | |
| − | + | The zero of an Abelian group $A$ (in additive notation) is an element, also denoted by $0$, satisfying $0+a = a$ for all $a \in A$. It is uniquely determined. | |
| − | The zero of | + | The zero of a ring (in particular, of a skew-field, i.e. division ring, or a field) is the zero of its additive group. The zero of a ring (like the number $0$) has the property of absorption under multiplication: $0\cdot a = a \cdot 0 = 0$. However, in an arbitrary ring the product of two non-zero elements may be zero. Such elements are called zero divisors (cf. [[Zero divisor|Zero divisor]]). Fields, skew-fields and integral domains do not have zero divisors. |
| − | + | A left zero of a semi-group $A$ (in multiplicative notation) is an element <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/z/z099/z099200/z09920013.png" /> such that $0\cdot a = 0$ for all $a \in A$. A right zero is defined by the dual property. If a semi-group has a two-sided zero (an element which is both a left and a right zero), then this element is unique. The zero of a ring is also the zero of its multiplicative semi-group. | |
| − | |||
| − | A left zero of a semi-group | ||
The zero of a lattice is its minimal element, if this exists. A complete lattice always has a zero: the intersection of all elements. | The zero of a lattice is its minimal element, if this exists. A complete lattice always has a zero: the intersection of all elements. | ||
| Line 19: | Line 18: | ||
For a zero object of a category, see [[Null object of a category|Null object of a category]]. | For a zero object of a category, see [[Null object of a category|Null object of a category]]. | ||
| − | The set of zeros of a function | + | The set of zeros of a function $f(x_1,\ldots,x_n)$ taking values in an Abelian group (ring, field, skew-field) $A$ is the collection of values of the variables $(x_1,\ldots,x_n)$ for which $f(x_1,\ldots,x_n) = 0$. |
| − | |||
====Comments==== | ====Comments==== | ||
| − | A subset of a topological space | + | A subset of a topological space $X$ is called a zero set if it is the set of zeros of some continuous real-valued function on $X$. Zero sets are an object of study in algebraic geometry (zero sets of systems of polynomials) and local analytic geometry (zero sets of systems of holomorphic functions and mappings). |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> N. Jacobson, "Basic algebra" , '''1''' , Freeman (1974) {{MR|0356989}} {{ZBL|0284.16001}} </TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> N. Jacobson, "Basic algebra" , '''1''' , Freeman (1974) {{MR|0356989}} {{ZBL|0284.16001}} </TD></TR></table> | ||
Revision as of 08:10, 27 December 2013
A (real or complex) number having the property that any number does not change if zero is added to it. It is denoted by the symbol $0$. The product of any number with zero is zero: $$0\cdot a = a \cdot 0 = 0 .$$
If the product of two numbers is zero, then one of them is zero (that is, $a\cdot b = 0$ implies $a=0$ or $b=0$). Division by zero is not defined. A direct generalization of this concept is that of the zero of an Abelian group.
The zero of an Abelian group $A$ (in additive notation) is an element, also denoted by $0$, satisfying $0+a = a$ for all $a \in A$. It is uniquely determined.
The zero of a ring (in particular, of a skew-field, i.e. division ring, or a field) is the zero of its additive group. The zero of a ring (like the number $0$) has the property of absorption under multiplication: $0\cdot a = a \cdot 0 = 0$. However, in an arbitrary ring the product of two non-zero elements may be zero. Such elements are called zero divisors (cf. Zero divisor). Fields, skew-fields and integral domains do not have zero divisors.
A left zero of a semi-group $A$ (in multiplicative notation) is an element 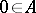 such that $0\cdot a = 0$ for all $a \in A$. A right zero is defined by the dual property. If a semi-group has a two-sided zero (an element which is both a left and a right zero), then this element is unique. The zero of a ring is also the zero of its multiplicative semi-group.
such that $0\cdot a = 0$ for all $a \in A$. A right zero is defined by the dual property. If a semi-group has a two-sided zero (an element which is both a left and a right zero), then this element is unique. The zero of a ring is also the zero of its multiplicative semi-group.
The zero of a lattice is its minimal element, if this exists. A complete lattice always has a zero: the intersection of all elements.
A zero of an algebraic system is an element picked out by a nullary operation (see Algebraic operation; Algebraic system). In the majority of examples considered above the zero is unique in the given system and even forms a one-element subsystem.
A zero is also called a null element.
For a zero object of a category, see Null object of a category.
The set of zeros of a function $f(x_1,\ldots,x_n)$ taking values in an Abelian group (ring, field, skew-field) $A$ is the collection of values of the variables $(x_1,\ldots,x_n)$ for which $f(x_1,\ldots,x_n) = 0$.
Comments
A subset of a topological space $X$ is called a zero set if it is the set of zeros of some continuous real-valued function on $X$. Zero sets are an object of study in algebraic geometry (zero sets of systems of polynomials) and local analytic geometry (zero sets of systems of holomorphic functions and mappings).
References
| [a1] | N. Jacobson, "Basic algebra" , 1 , Freeman (1974) MR0356989 Zbl 0284.16001 |
Zero. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Zero&oldid=31206