Difference between revisions of "Ermakov convergence criterion"
From Encyclopedia of Mathematics
(Importing text file) |
|||
| Line 1: | Line 1: | ||
| − | + | {{MSC|40A05}} | |
| + | {{TEX|done}} | ||
| − | + | A criterion for the convergence of a series $\sum_n f(n)$, where $f:[1, \infty[\to [0, \infty[$ is a monotone decreasing function, established by | |
| − | + | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e036/e036200/e0362001.png" /> be a positive decreasing function for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/e/e036/e036200/e0362002.png" />. If the inequality V.P. Ermakov in {{Cite|Er}}. If there is $\lambda< 1$ such that | |
| − | + | \[ | |
| − | + | \frac{e^x f(e^x)}{f(x)} < \lambda | |
| − | + | \] | |
| − | + | for sufficiently large $x$, then the series $\sum_n f(n)$ converges. If instead | |
| − | + | \[ | |
| − | + | \frac{e^x f(e^x)}{f(x)}\geq 1 | |
| − | + | \] | |
| − | + | for all sufficiently large $x$, then the series diverges. In particular the convergence or divergence of the series can be decided of the limit | |
| − | + | \[ | |
| − | then the series | + | \lim_{x\to\infty} \frac{e^x f(e^x)}{f(x)} |
| − | + | \] | |
| − | + | exists and differs from 1. | |
| − | |||
| − | then the series | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| + | Ermakov's criterion can be derived from the [[Integral test|integral test]]. | ||
====References==== | ====References==== | ||
| − | + | {| | |
| + | |- | ||
| + | |valign="top"|{{Ref|Br}}|| T.J. Bromwich, "An introduction to the theory of infinite series" , Macmillan (1947) | ||
| + | |- | ||
| + | |valign="top"|{{Ref|Er}}|| V.P. Ermakov, "A new criterion for convergence and divergence of infinite series of constant sign" , Kiev (1872) (In Russian) | ||
| + | |- | ||
| + | |} | ||
Revision as of 13:31, 10 December 2013
2020 Mathematics Subject Classification: Primary: 40A05 [MSN][ZBL]
A criterion for the convergence of a series $\sum_n f(n)$, where $f:[1, \infty[\to [0, \infty[$ is a monotone decreasing function, established by
Let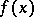 
be a positive decreasing function for 
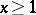. If the inequality V.P. Ermakov in [Er]. If there is $\lambda< 1$ such that
\[
\frac{e^x f(e^x)}{f(x)} < \lambda
\]
for sufficiently large $x$, then the series $\sum_n f(n)$ converges. If instead
\[
\frac{e^x f(e^x)}{f(x)}\geq 1
\]
for all sufficiently large $x$, then the series diverges. In particular the convergence or divergence of the series can be decided of the limit
\[
\lim_{x\to\infty} \frac{e^x f(e^x)}{f(x)}
\]
exists and differs from 1.
Ermakov's criterion can be derived from the integral test.
References
| [Br] | T.J. Bromwich, "An introduction to the theory of infinite series" , Macmillan (1947) |
| [Er] | V.P. Ermakov, "A new criterion for convergence and divergence of infinite series of constant sign" , Kiev (1872) (In Russian) |
How to Cite This Entry:
Ermakov convergence criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ermakov_convergence_criterion&oldid=30931
Ermakov convergence criterion. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Ermakov_convergence_criterion&oldid=30931
This article was adapted from an original article by L.D. Kudryavtsev (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article