Model theory

The part of mathematical logic studying mathematical models (cf. Model (in logic)).

The origins of model theory go back to the 1920's and 1930's, when the following two fundamental theorems were proved.

Theorem 1

(Gödel compactness theorem). If each finite subcollection of a collection $T$ of propositions in a first-order language is consistent, then the whole collection $T$ is consistent (see [1]).

Theorem 2

(Löwenheim–Skolem theorem). If a collection of propositions in a first-order language of signature has an infinite model, then it has a model of any infinite cardinality not less than the cardinality of .

Theorem 1 has had extensive application in algebra. On the basis of this theorem, A.I. Mal'tsev created a method of proof of local theorems in algebra (see Mal'tsev local theorems).

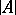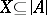Let be an algebraic system of signature , let be the underlying set of , let , let 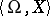denote the signature obtained from by the addition of symbols for distinguished elements 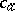for all 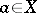, and let 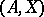denote the algebraic system of signature 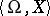which is an enrichment of 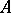in which for each 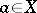the symbol 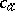is interpreted by the element . The set 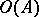of all closed formulas of the signature 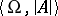in a first-order language which are true in the system 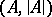is called the elementary diagram of the algebraic system 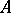(or the description of the algebraic system 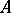), and the set 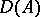of those formulas from 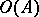which are either atomic or the negation of an atomic formula is called the diagram of 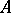. An algebraic system 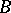is called an elementary extension o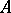f if 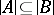and if 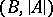is a model for 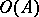. In this case 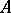is called an elementary subsystem of 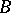. For example, the set of rational numbers with the usual order relation is an elementary subsystem of the system of real numbers with the usual order relation.

A subsystem 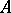of an algebraic system of signature is an elementary subsystem of 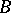if and only if for each closed formula 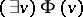in the first-order language of signature 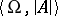which is true in 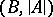there is an 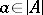such that 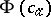is true in 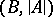. It follows at once from this criterion that the union of an increasing chain of elementary subsystems is an elementary extension of each of these subsystems. If a closed 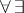-formula in a first-order language is true in every system of an increasing chain of systems, then it is true in the union of the chain (see [1], [8]).

Let the signature contain a one-place relation symbol 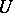. One says that a model 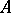of a theory 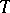of signature has type 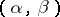if the cardinality of 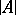is equal to 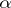and if the cardinality of 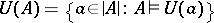is equal to 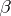. Vaught's theorem: If an elementary theory 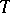of countable signature has a model of typ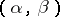e where , then 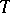has a model of type 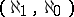(see [7], [8], [10]). Under the assumption that the generalized continuum hypothesis holds, an elementary theory of countable signature has models of types 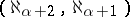for each 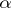, if it has a model of type 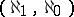(see [10]). Under the same assumption the theory 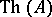, where the signature of 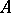is 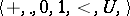, 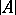is the set of all real numbers, 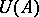the set of all integers, and 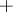, , , , 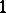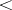are defined in the usual way, does not have a model of type .

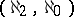Let 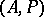denote the enrichment of the algebraic system 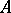by a predicate 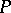, and let 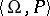be the signature obtained from by the addition of the predicate symbol 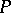. In many cases it is important to understand when in each member of a class 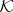of algebraic systems of signature 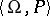the predicate 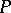is given by a formula in the first-order language of the signature . A partial answer to this question is given by Beth's definability theorem: There exists a formula in the first-order language of signature such that the formula 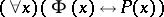is true for all members of an axiomatizable class 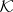of signature 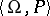if and only if the set 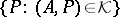contains at most one element for each algebraic system 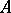of signature (see [2], [8]).

Much research in model theory is connected with the study of properties preserved under operations on algebraic systems. The most important operations include homomorphism, direct and filtered products.

A statement 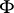is said to be stable with respect to homomorphisms if the truth of 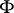in an algebraic system 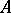implies the truth of 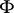in all epimorphic images of 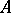. A formula 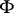in a first-order language is called positive if 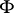does not contain negation and implication signs. It has been proved (see [1], [8]) that a statement 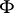in a first-order language is stable relative to homomorphisms if and only if 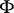is equivalent to a positive statement. A similar theorem holds for the language .

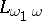A formula 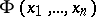in a first-order language of signature is called a Horn formula it it can be obtained by conjunction and quantification from formulas of the form 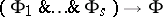, , 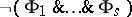where 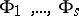are atomic formulas in the first-order language of . Examples of Horn formulas are identities and quasi-identities. Central in the theory of ultraproducts is the theorem of J. Łos: Every formula in a first-order language is stable with respect to any ultrafilter (see [1]). A formula in a first-order language is conditionally stable with respect to any filter if and only if it is equivalent to a Horn formula. 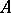There is the following theorem (see [9]): Two algebraic systems and 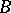of signature are elementarily equivalent if and only if there is an ultrafilter 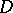on a set 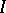such that 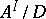and 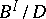are isomorphic. The cardinality of a filtered product is countably infinite if for each natural number the number of factors of cardinality is finite. If for each natural number the set of indices for which the corresponding factors have cardinality does not belong to 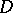, then the cardinality of the ultraproduct with respect to a non-principal ultrafilter 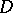on a countable set 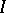is equal to that of the continuum. For each infinite set 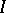of cardinality 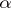there is a filter 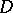on such that for each filter 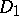on 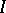containing 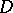, and each infinite set 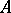, the cardinality of 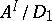is not less than 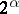(see [1]).

Many applications have been found for the Ehrenfeucht–Mostowski theorem on the existence of models with a large number of automorphisms (see [3]): For any totally ordered set 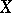in an axiomatizable class 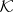of algebraic systems containing an infinite system, there is a system 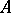such that 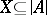and such that each order-preserving one-to-one mapping of 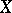onto 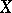can be extended to an automorphism of .

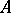The major notions in model theory are those of universal, homogeneous and saturated systems. Let 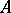and 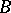be algebraic systems of a signature . A mapping 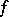of a set 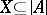into a set is called elementary if for each formula 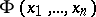in the first-order language of the signature and any 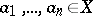the equivalence 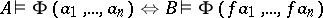holds. A system 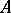is called 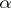-universal if for every system 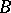that is elementarily equivalent to 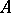and of cardinality not exceeding 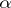, there is an elementary mapping from 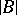into 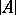. A system 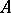is called 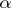-homogeneous if for every set 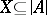of cardinality less than 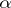, every elementary mapping from 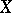into 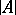can be extended to an elementary mapping of 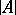onto 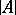(that is, to an automorphism of 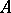). A system 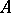of signature is called 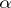-saturated if for every set 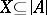of cardinality less than 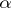and every collection 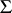of formulas in the first-order language of the signature 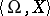not containing free variables other than 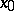, 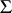finitely satisfiable in 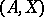implies that 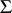is satisfiable in 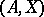. A system is called universal (respectively, homogeneous or saturated) if 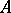is 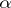-universal (respectively, 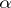-homogeneous or 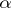-saturated), where 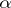is the cardinality of 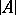. A system is saturated if and only if it is simultaneously universal and homogeneous. Two elementary equivalent saturated systems of the same cardinality are isomorphic (see [3]). All uncountable models of elementary theories which are categorical in uncountable cardinalities (cf. Categoricity in cardinality) and of countable signature are saturated (Morley's theorem, see [3], [8]). A large number of examples of 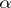-saturated systems is given by ultraproducts. For example, if 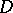is a non-principal ultrafilter on a countable set 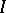, the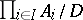n is an 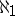-saturated system for any algebraic system 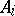(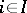) of a countable signature .

The basic problems of model theory are the study of the expressive possibilities of a formalized language and the study of classes of structures defined by means of such a language. Some important properties of stable theories have been found, and the classes of categorical and superstable theories have been studied in even more detail.

The basic apparatus for the study of stable theories is the classification of formulas and locally consistent sets of formulas in these theories. Such a classification can be obtained by means of ascribing to formulas their ranks. Such ranks are usually ordinals and the ranking functions are given with the help of special topologies and other means. The study of ranking functions and their improvements is a rich source of information on the theories.

In the study of classes of models one is concerned with the number of distinct models, up to isomorphism, of a theory of a given cardinality, the existence of special models, for example, simple, minimal, saturated, homogeneous, universal, etc., and one creates means for constructing them.

The classical examples of application of methods of model theory are the papers of A. Robinson and his school, which developed an independent science — non-standard analysis; from the work of Mal'tsev and his school the applications of model-theoretic methods to topological algebra have been developed; the latest results on the properties of stable theories have been used in the study of concrete algebraic questions.

The above problems arose also in the study of various non-elementary languages, for example, obtained by the addition of new quantifiers, the introduction of infinite expressions, modalities, etc.

References

[1]	A.I. Mal'tsev, "Algebraic systems" , Springer (1973) (Translated from Russian)
[2]	A. Robinson, "Introduction to model theory and to the metamathematics of algebra" , North-Holland (1963)
[3]	M.A. Taitslin, "Model theory" , Novosibirsk (1970) (In Russian)
[4]	Yu.L. Ershov, "Decidability problems and constructive models" , Moscow (1980) (In Russian)
[5]	Yu.A. Palyutin, "Mathematical logic" , Moscow (1979) (In Russian)
[6]	Yu.L. Ershov, I.A. Lavrov, A.D. Taimanov, M.A. Taitslin, "Elementary theories" Russian Math. Surveys , 20 : 4 (1965) pp. 35–105 Uspekhi Mat. Nauk , 20 : 4 (1965) pp. 37–108
[7]	A.I. Mal'tsev, "Some problems in the theory of classes of models" , Proc. 4-th All-Union Math. Congress (1961) , 1 , Leningrad (1963) pp. 169–198 (In Russian) (Transl. in: Amer. Math. Soc. Transl. (2) 83 (1969), 1–48)
[8]	C.C. Chang, H.J. Keisler, "Model theory" , North-Holland (1973)
[9]	G.E. Sacks, "Saturated model theory" , Benjamin (1972)
[10]	R.L. Vaught, "Denumerable models of complete theories" , Infinitistic methods. Proc. Symp. Foundations of Math. Warsaw, 1959 , Pergamon (1961) pp. 303–321
[11]	M. Morley, R. Vaught, "Homogeneous universal models" Math. Scand. , 11 : 1 (1962) pp. 37–57
[12]	M. Morley, "Categoricity in power" Trans. Amer. Math. Soc. , 114 : 2 (1965) pp. 514–538
[13]	S. Shelah, "Classification theory and the number of non-isomorphic models" , North-Holland (1978)
[14]	J.L. Bell, A.B. Slomson, "Models and ultraproducts: an introduction" , North-Holland (1971)

Comments

Theorem 1 was proved by K. Gödel in [a1].

Let 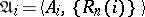, , 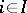be a collection of relational structures of the same type (algebraic systems of the same signature). (I.e. the 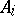are sets, the 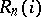relations.) Let 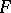be an ultrafilter on the index set 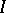. Then the ultraproduct 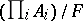is a relational structure of the same type. (Cf. (the editorial comments to) Ultrafilter for the definition of ultraproduct.)

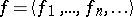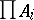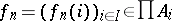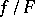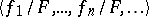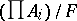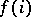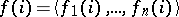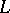A precise formulation of Łos' theorem is now as follows (cf. [a8] or [a9]). Let be a sequence of elements from , i.e. for all . Let be the sequence of elements from and let be the sequence . Then for any formula from the language for which the 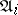are interpretations,

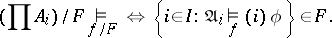Łos' theorem is also called the fundamental theorem on ultraproducts.

The theorem to the effect that two algebraic systems 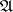and 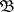are equivalent if and only if they have isomorphic ultrapowers is known as the Keisler ultrapower theorem.

One of the basic applications of logic to algebra is the work by J. Ax and S. Kochen [a2].

See [a3] for the model theory of infinitary languages; [a4], [a5] for stability theory; and [a6], [a7] for categorical model theory.

The Gödel compactness theorem and the Löwenheim–Skolem theorem are in the Russian literature sometimes known as the Gödel–Mal'tsev theorem and the Löwenheim–Skolem–Mal'tsev theorem, respectively.

References

[a1]	K. Gödel, "Die Vollständigheit der Axiome des logischen Funktionenkalküls" Monatshefte für Math. und Physik , 37 (1930) pp. 344–360
[a2]	J. Ax, S. Kochen, "Diophantine problems over local fields III: decidable fields" Ann. of Math. , 83 (1966) pp. 437–456
[a3]	M.A. Dickmann, "Large infinitary languages" , North-Holland (1975)
[a4]	A. Pillay, "An introduction to stability theory" , Oxford Univ. Press (1985)
[a5]	J.T. Baldwin, "Fundamentals of stability theory" , Springer (1988)
[a6]	G.E. Reges, "First order categorical logic" , Lect. notes in math. , 611 , Springer (1977)
[a7]	J. Lambek, P. Scott, "Higher order categorical logic" , Cambridge Univ. Press (1986)
[a8]	J.L. Bell, A.B. Slomson, "Models and ultraproducts" , North-Holland (1969)
[a9]	W.W. Comfort, S. Negrepontis, "The theory of ultrafilters" , Springer (1974) pp. §11