Namespaces
Variants
Actions

Difference between revisions of "Möbius function"

From Encyclopedia of Mathematics
Jump to: navigation, search
(Remove material that does not appear to be attributed to a scholarly source)
Line 1: Line 1:
−
 
 
An [[Arithmetic function|arithmetic function]] of natural argument: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064280/m0642801.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064280/m0642802.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064280/m0642803.png" /> is divisible by the square of a prime number, otherwise <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064280/m0642804.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064280/m0642805.png" /> is the number of prime factors of the number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064280/m0642806.png" />. This function was introduced by A. Möbius in 1832.
 
An [[Arithmetic function|arithmetic function]] of natural argument: <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064280/m0642801.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064280/m0642802.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064280/m0642803.png" /> is divisible by the square of a prime number, otherwise <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064280/m0642804.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064280/m0642805.png" /> is the number of prime factors of the number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064280/m0642806.png" />. This function was introduced by A. Möbius in 1832.
  
Line 7: Line 6:
  
 
where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064280/m06428010.png" /> is a constant. The fact that the mean value tends to zero as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064280/m06428011.png" /> implies an asymptotic law for the [[Distribution of prime numbers|distribution of prime numbers]] in the natural series.
 
where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064280/m06428010.png" /> is a constant. The fact that the mean value tends to zero as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064280/m06428011.png" /> implies an asymptotic law for the [[Distribution of prime numbers|distribution of prime numbers]] in the natural series.
−
 
−
The Möbius function is related to the Riemann zeros via the formula
 
−
 
−
\begin{equation} \sum_{n=1}^{\infty}\frac{\mu(n)}{\sqrt{n}} g \log n = \sum_t \frac{h(t)}{\zeta'(1/2+it)}+2\sum_{n=1}^\infty \frac{ (-1)^{n} (2\pi )^{2n}}{(2n)! \zeta(2n+1)}\int_{-\infty}^{\infty}g(x) e^{-x(2n+1/2)} \, dx,\end{equation}
 
  
 
====References====
 
====References====
 
<table><TR><TD valign="top">[1]</TD> <TD valign="top">  I.M. Vinogradov,  "Elements of number theory" , Dover, reprint  (1954)  (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top">  A. Walfisz,  "Weylsche Exponentialsummen in der neueren Zahlentheorie" , Deutsch. Verlag Wissenschaft.  (1963)</TD></TR></table>
 
<table><TR><TD valign="top">[1]</TD> <TD valign="top">  I.M. Vinogradov,  "Elements of number theory" , Dover, reprint  (1954)  (Translated from Russian)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top">  A. Walfisz,  "Weylsche Exponentialsummen in der neueren Zahlentheorie" , Deutsch. Verlag Wissenschaft.  (1963)</TD></TR></table>
  
−
[3] Jose Javier Garcia Moreta "http://www.prespacetime.com/index.php/pst/issue/view/42 Borel Resummation & the Solution of Integral Equations
+
 
  
 
====Comments====
 
====Comments====

Revision as of 21:35, 31 August 2013

An arithmetic function of natural argument: , 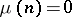if is divisible by the square of a prime number, otherwise , where is the number of prime factors of the number . This function was introduced by A. Möbius in 1832.

The Möbius function is a multiplicative arithmetic function; if 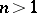. It is used in the study of other arithmetic functions; it appears in inversion formulas (see, e.g. Möbius series). The following estimate is known for the mean value of the Möbius function [2]:

where is a constant. The fact that the mean value tends to zero as 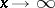implies an asymptotic law for the distribution of prime numbers in the natural series.

References

[1] I.M. Vinogradov, "Elements of number theory" , Dover, reprint (1954) (Translated from Russian)
[2] A. Walfisz, "Weylsche Exponentialsummen in der neueren Zahlentheorie" , Deutsch. Verlag Wissenschaft. (1963)


Comments

The multiplicative arithmetic functions form a group under the convolution product 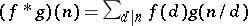. The Möbius function is in fact the inverse of the constant multiplicative function 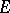(defined by 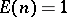for all ) under this convolution product. From this there follows many "inversion formulas" , cf. e.g. Möbius series.

References

[a1] G.H. Hardy, E.M. Wright, "An introduction to the theory of numbers" , Clarendon Press (1979)
How to Cite This Entry:
Möbius function. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=M%C3%B6bius_function&oldid=30292
This article was adapted from an original article by N.I. Klimov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article
Retrieved from "https://encyclopediaofmath.org/index.php?title=Möbius_function&oldid=30292"