Difference between revisions of "Pseudo-prime"
(Importing text file) |
(converting to LaTeX) |
||
| Line 1: | Line 1: | ||
| − | |||
| − | + | Traditionally, a composite natural number $n$ is called a pseudo-prime if $2^{n-1} \equiv 1$ modulo $n$, for it has long been known that primes have this property. (The term is apparently due to D.H. Lehmer.) There are infinitely many such $n$, the first five being | |
| + | $$ | ||
| + | 341,\,561,\,645,\,1105,\,1387\ . | ||
| + | $$ | ||
More recently, the concept has been extended to include any composite number that acts like a prime in some realization of a [[Probabilistic primality test|probabilistic primality test]]. That is, it satisfies some easily computable necessary, but not sufficient, condition for primality. Pseudo-primes in this larger sense include: | More recently, the concept has been extended to include any composite number that acts like a prime in some realization of a [[Probabilistic primality test|probabilistic primality test]]. That is, it satisfies some easily computable necessary, but not sufficient, condition for primality. Pseudo-primes in this larger sense include: | ||
| − | 1) ordinary base- | + | 1) ordinary base-$b$ pseudo-primes, satisfying $b^{n-1}\equiv1$ modulo $n$; |
| − | 2) Euler base- | + | 2) Euler base-$b$ pseudo-primes, whose [[Jacobi symbol|Jacobi symbol]] with $b$ satisfies |
| + | $$ | ||
| + | b^{(n-1)/2} \equiv\left({\frac{b}{n}}\right) = \pm 1 | ||
| + | $$ | ||
| − | + | 3) strong base-$b$ pseudo-primes, for which the sequence $b^{s.2^i}$ modulo $n$ for $i=0,\ldots, r$ is either always $1$, or contains $-1$. (Here $n-1 = 2^r.s$ with $s$ odd.) | |
| − | |||
| − | 3) strong base- | ||
For each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110270/p11027023.png" />, the implications 3)<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110270/p11027024.png" />2)<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110270/p11027025.png" />1) hold. A number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110270/p11027026.png" /> that is an ordinary base-<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110270/p11027027.png" /> pseudo-prime for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110270/p11027028.png" /> prime to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110270/p11027029.png" /> is called a [[Carmichael number|Carmichael number]]. Analogous numbers for the other two categories do not exist. | For each <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110270/p11027023.png" />, the implications 3)<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110270/p11027024.png" />2)<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110270/p11027025.png" />1) hold. A number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110270/p11027026.png" /> that is an ordinary base-<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110270/p11027027.png" /> pseudo-prime for all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110270/p11027028.png" /> prime to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/p/p110/p110270/p11027029.png" /> is called a [[Carmichael number|Carmichael number]]. Analogous numbers for the other two categories do not exist. | ||
Revision as of 17:10, 25 August 2013
Traditionally, a composite natural number $n$ is called a pseudo-prime if $2^{n-1} \equiv 1$ modulo $n$, for it has long been known that primes have this property. (The term is apparently due to D.H. Lehmer.) There are infinitely many such $n$, the first five being $$ 341,\,561,\,645,\,1105,\,1387\ . $$
More recently, the concept has been extended to include any composite number that acts like a prime in some realization of a probabilistic primality test. That is, it satisfies some easily computable necessary, but not sufficient, condition for primality. Pseudo-primes in this larger sense include:
1) ordinary base-$b$ pseudo-primes, satisfying $b^{n-1}\equiv1$ modulo $n$;
2) Euler base-$b$ pseudo-primes, whose Jacobi symbol with $b$ satisfies $$ b^{(n-1)/2} \equiv\left({\frac{b}{n}}\right) = \pm 1 $$
3) strong base-$b$ pseudo-primes, for which the sequence $b^{s.2^i}$ modulo $n$ for $i=0,\ldots, r$ is either always $1$, or contains $-1$. (Here $n-1 = 2^r.s$ with $s$ odd.)
For each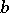 
, the implications 3)
2)
1) hold. A number 
that is an ordinary base-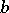
pseudo-prime for all 
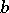prime to 
is called a Carmichael number. Analogous numbers for the other two categories do not exist.
For a thorough empirical study of pseudo-primes, see [a4]. Lists of pseudo-primes to various small bases can be found in [a6].
The concept of a pseudo-prime has been generalized to include primality tests based on finite fields and elliptic curves (cf. also Finite field; Elliptic curve). For reviews of this work, see [a3], [a5].
The complementary concept is also of interest. The base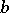 
is called a (Fermat) witness for 
if 
is composite but not a base-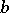
pseudo-prime. Euler and strong witnesses are similarly defined. If 
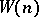, the smallest strong witness for 
, grows sufficiently slowly, there is a polynomial-time algorithm for primality. It is known that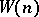 
is not bounded [a2], but if an extended version of the Riemann hypothesis (cf. Riemann hypotheses) holds, then 
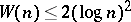[a1].
References
| [a1] | E. Bach, "Analytic methods in the analysis and design of number-theoretic algorithms" , MIT (1985) |
| [a2] | W.R. Alford, A. Granville, C. Pomerance, "On the difficulty of finding reliable witnesses" , Algorithmic Number Theory, First Internat. Symp., ANTS-I , Lecture Notes in Computer Science , 877 , Springer (1994) pp. 1–16 |
| [a3] | F. Morain, "Pseudoprimes: a survey of recent results" , Proc. Eurocode '92 , Springer (1993) pp. 207–215 |
| [a4] | C. Pomerance, J.L. Selfridge, S.S. Wagstaff, Jr., "The pseudoprimes to  " Math. Comp. , 35 (1980) pp. 1003–1026 |
| [a5] | P. Ribenboim, "The book of prime number records" , Springer (1989) (Edition: Second) |
| [a6] | N.J.A. Sloane, S. Plouffe, "The encyclopedia of integer sequences" , Acad. Press (1995) |
Pseudo-prime. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Pseudo-prime&oldid=30229