Difference between revisions of "Carmichael number"
(Importing text file) |
m (correct statement of Fermat's Little Theorem: a^p == a mod p) |
||
| Line 1: | Line 1: | ||
| − | A composite natural number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c110/c110100/c1101001.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c110/c110100/c1101002.png" /> modulo <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c110/c110100/c1101003.png" />, whenever <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c110/c110100/c1101004.png" /> is relatively prime to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c110/c110100/c1101005.png" />. Thus they are pseudo-primes (cf. [[Pseudo-prime|Pseudo-prime]]) for every such base <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c110/c110100/c1101006.png" />. These numbers play a role in the theory of probabilistic primality tests (cf. [[Probabilistic primality test|Probabilistic primality test]]), as they show that Fermat's theorem, to wit | + | A composite natural number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c110/c110100/c1101001.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c110/c110100/c1101002.png" /> modulo <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c110/c110100/c1101003.png" />, whenever <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c110/c110100/c1101004.png" /> is relatively prime to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c110/c110100/c1101005.png" />. Thus they are pseudo-primes (cf. [[Pseudo-prime|Pseudo-prime]]) for every such base <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c110/c110100/c1101006.png" />. These numbers play a role in the theory of probabilistic primality tests (cf. [[Probabilistic primality test|Probabilistic primality test]]), as they show that Fermat's theorem, to wit $ a^p \equiv a $ modulo <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c110/c110100/c1101008.png" />, whenever <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c110/c110100/c1101009.png" /> is prime and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c110/c110100/c11010010.png" /> modulo <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c110/c110100/c11010011.png" />, is not a sufficient criterion for primality (cf. also [[Fermat little theorem|Fermat little theorem]]). |
The first five Carmichael numbers are | The first five Carmichael numbers are | ||
Revision as of 21:28, 21 February 2013
A composite natural number  for which
for which 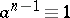 modulo
modulo  , whenever
, whenever  is relatively prime to
is relatively prime to  . Thus they are pseudo-primes (cf. Pseudo-prime) for every such base
. Thus they are pseudo-primes (cf. Pseudo-prime) for every such base  . These numbers play a role in the theory of probabilistic primality tests (cf. Probabilistic primality test), as they show that Fermat's theorem, to wit $ a^p \equiv a $ modulo
. These numbers play a role in the theory of probabilistic primality tests (cf. Probabilistic primality test), as they show that Fermat's theorem, to wit $ a^p \equiv a $ modulo 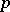 , whenever
, whenever 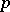 is prime and
is prime and 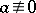 modulo
modulo 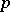 , is not a sufficient criterion for primality (cf. also Fermat little theorem).
, is not a sufficient criterion for primality (cf. also Fermat little theorem).
The first five Carmichael numbers are
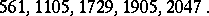 |
R.D. Carmichael [a2] characterized them as follows. Let 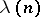 be the exponent of the multiplicative group of integers modulo
be the exponent of the multiplicative group of integers modulo  , that is, the least
, that is, the least 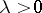 making all
making all 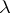 th powers in the group equal to
th powers in the group equal to 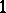 . (This is readily computed from the prime factorization of
. (This is readily computed from the prime factorization of  .) Then a composite natural number
.) Then a composite natural number  is Carmichael if and only if
is Carmichael if and only if 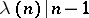 . From this it follows that every Carmichael number is odd, square-free, and has at least
. From this it follows that every Carmichael number is odd, square-free, and has at least  distinct prime factors.
distinct prime factors.
Let 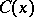 denote the number of Carmichael numbers
denote the number of Carmichael numbers 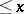 . W.R. Alford, A. Granville and C. Pomerance [a1] proved that
. W.R. Alford, A. Granville and C. Pomerance [a1] proved that 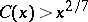 for sufficiently large
for sufficiently large  . This settled a long-standing conjecture that there are infinitely many Carmichael numbers. It is believed on probabilistic grounds that
. This settled a long-standing conjecture that there are infinitely many Carmichael numbers. It is believed on probabilistic grounds that 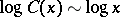 [a4].
[a4].
There is apparently no better way to compute 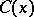 than to make a list of the Carmichael numbers up to
than to make a list of the Carmichael numbers up to  . The most exhaustive computation to date (1996) is that of R.G.E. Pinch, who used the methods of [a3] to determine that
. The most exhaustive computation to date (1996) is that of R.G.E. Pinch, who used the methods of [a3] to determine that 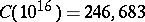 .
.
References
| [a1] | W.R. Alford, A. Granville, C. Pomerance, "There are infinitely many Carmichael numbers" Ann. of Math. , 140 (1994) pp. 703–722 |
| [a2] | R.D. Carmichael, "Note on a new number theory function" Bull. Amer. Math. Soc. , 16 (1910) pp. 232–238 (See also: Amer. Math. Monthly 19 (1912), 22–27) |
| [a3] | R.G.E. Pinch, "The Carmichael numbers up to 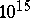 " Math. Comp. , 61 (1993) pp. 381–391 " Math. Comp. , 61 (1993) pp. 381–391 |
| [a4] | C. Pomerance, J.L. Selfridge, S.S. Wagstaff, Jr., "The pseudoprimes to 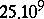 " Math. Comp. , 35 (1980) pp. 1003–1026 " Math. Comp. , 35 (1980) pp. 1003–1026 |
Carmichael number. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Carmichael_number&oldid=29456