Difference between revisions of "Prime ideal"
From Encyclopedia of Mathematics
(Importing text file) |
m (→Comments: about m system ststement) |
||
| Line 4: | Line 4: | ||
====Comments==== | ====Comments==== | ||
| − | + | This assumes that the empty set is an m system by default. | |
====References==== | ====References==== | ||
<table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L.H. Rowen, "Ring theory" , '''I''' , Acad. Press (1988) pp. 163</TD></TR></table> | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> L.H. Rowen, "Ring theory" , '''I''' , Acad. Press (1988) pp. 163</TD></TR></table> | ||
Revision as of 21:49, 11 December 2012
A two-sided ideal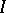 
of a ring 
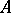such that the inclusion 
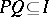for any two-sided ideals 
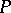and 
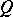of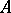 
implies that either 
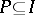or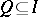 
. An ideal 
of a ring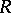 
is prime if and only if the set 
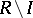is an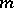 
-system, i.e. for any 
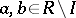there exists an 
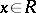such that 
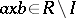. An ideal 
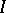of a ring 
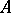is prime if and only if the quotient ring by it is a prime ring.
Comments
This assumes that the empty set is an m system by default.
References
| [a1] | L.H. Rowen, "Ring theory" , I , Acad. Press (1988) pp. 163 |
How to Cite This Entry:
Prime ideal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Prime_ideal&oldid=29171
Prime ideal. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Prime_ideal&oldid=29171
This article was adapted from an original article by K.A. Zhevlakov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article