Difference between revisions of "Non-central chi-squared distribution"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (dead link removed) |
||
| Line 5: | Line 5: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066960/n0669604.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066960/n0669604.png" /></td> </tr></table> | ||
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066960/n0669605.png" /> is the number of degrees of freedom and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066960/n0669606.png" /> the parameter of non-centrality. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066960/n0669607.png" /> this density is that of the ordinary (central) [[ | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066960/n0669605.png" /> is the number of degrees of freedom and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066960/n0669606.png" /> the parameter of non-centrality. For <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066960/n0669607.png" /> this density is that of the ordinary (central) [[Chi-squared distribution| "chi-squared" distribution]]. The [[Characteristic function|characteristic function]] of a non-central "chi-squared" distribution is |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066960/n0669608.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066960/n0669608.png" /></td> </tr></table> | ||
Revision as of 11:49, 20 October 2012
non-central 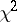 -distribution
-distribution
A continuous probability distribution concentrated on the positive semi-axis 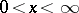 with density
with density
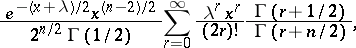 |
where  is the number of degrees of freedom and
is the number of degrees of freedom and 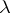 the parameter of non-centrality. For
the parameter of non-centrality. For 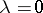 this density is that of the ordinary (central) "chi-squared" distribution. The characteristic function of a non-central "chi-squared" distribution is
this density is that of the ordinary (central) "chi-squared" distribution. The characteristic function of a non-central "chi-squared" distribution is
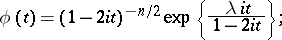 |
the mathematical expectation and variance (cf. Dispersion) are 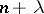 and
and 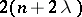 , respectively. A non-central "chi-squared" distribution belongs to the class of infinitely-divisible distributions (cf. Infinitely-divisible distribution).
, respectively. A non-central "chi-squared" distribution belongs to the class of infinitely-divisible distributions (cf. Infinitely-divisible distribution).
As a rule, a non-central "chi-squared" distribution appears as the distribution of the sum of squares of independent random variables 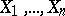 having normal distributions with non-zero means
having normal distributions with non-zero means 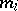 and unit variance; more precisely, the sum
and unit variance; more precisely, the sum 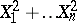 has a non-central "chi-squared" distribution with
has a non-central "chi-squared" distribution with  degrees of freedom and non-centrality parameter
degrees of freedom and non-centrality parameter 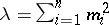 . The sum of several mutually independent random variables with a non-central "chi-squared" distribution has a distribution of the same type and its parameters are the sums of the corresponding parameters of the summands.
. The sum of several mutually independent random variables with a non-central "chi-squared" distribution has a distribution of the same type and its parameters are the sums of the corresponding parameters of the summands.
If  is even, then the distribution function of a non-central "chi-squared" distribution
is even, then the distribution function of a non-central "chi-squared" distribution 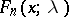 is given by
is given by 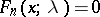 for
for 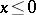 and for
and for 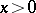 by
by
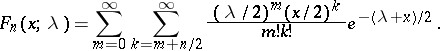 |
This formula establishes a link between a non-central "chi-squared" distribution and a Poisson distribution. Namely, if 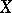 and
and 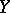 have Poisson distributions with parameters
have Poisson distributions with parameters 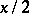 and
and 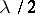 , respectively, then for any positive integer
, respectively, then for any positive integer 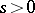 ,
,
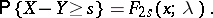 |
A non-central "chi-squared" distribution often arises in problems of mathematical statistics concerned with the study of the power of tests of "chi-squared" type. Since tables of non-central "chi-squared" distributions are fairly complete, various approximations by means of a "chi-squared" and a normal distribution are widely used in statistical applications.
References
| [1] | L.N. Bol'shev, N.V. Smirnov, "Tables of mathematical statistics" , Libr. math. tables , 46 , Nauka (1983) (In Russian) (Processed by L.S. Bark and E.S. Kedrova) |
| [2] | M.G. Kendall, A. Stuart, "The advanced theory of statistics" , 2. Inference and relationship , Griffin (1979) |
| [3] | P.B. Patnaik, "The non-central 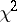 - and - and 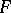 -distributions and their applications" Biometrica , 36 (1949) pp. 202–232 -distributions and their applications" Biometrica , 36 (1949) pp. 202–232 |
Comments
References
| [a1] | N.L. Johnson, S. Kotz, "Distributions in statistics" , 2. Continuous univariate distributions , Wiley (1970) |
Non-central chi-squared distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Non-central_chi-squared_distribution&oldid=28548