Difference between revisions of "Newton method"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 30: | Line 30: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> L.V. Kantorovich, "Functional analysis and applied mathematics" ''Nat. Bur. Sci. Rep.'' , '''1509''' (1952) ''Uspekhi Mat. Nauk'' , '''3''' : 6 (1948) pp. 89–185</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> L.V. Kantorovich, G.P. Akilov, "Functionalanalysis in normierten Räumen" , Akademie Verlag (1964) (Translated from Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> L. Collatz, "Funktionalanalysis und numerische Mathematik" , Springer (1964)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> M.A. Krasnosel'skii, G.M. Vainikko, P.P. Zabreiko, et al., "Approximate solution of operator equations" , Wolters-Noordhoff (1972) (Translated from Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian)</TD></TR></table> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> L.V. Kantorovich, "Functional analysis and applied mathematics" ''Nat. Bur. Sci. Rep.'' , '''1509''' (1952) ''Uspekhi Mat. Nauk'' , '''3''' : 6 (1948) pp. 89–185 {{MR|0053389}} {{ZBL|0034.21203}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> L.V. Kantorovich, G.P. Akilov, "Functionalanalysis in normierten Räumen" , Akademie Verlag (1964) (Translated from Russian) {{MR|}} {{ZBL|}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> L. Collatz, "Funktionalanalysis und numerische Mathematik" , Springer (1964) {{MR|0165651}} {{ZBL|0139.09802}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> M.A. Krasnosel'skii, G.M. Vainikko, P.P. Zabreiko, et al., "Approximate solution of operator equations" , Wolters-Noordhoff (1972) (Translated from Russian) {{MR|385655}} {{ZBL|0231.41024}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian) {{MR|0362811}} {{ZBL|0524.65001}} </TD></TR></table> |
| Line 38: | Line 38: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P. Lax, S. Burstein, A. Lax, "Calculus with applications and computing" , New York Univ. Inst. Math. Mech. (1972)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.E., jr. Dennis, R. Schnable, "Least change secant updates for quasi-Newton methods" ''SIAM Review'' , '''21''' (1979) pp. 443–459</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J.M. Ortega, W.C. Rheinboldt, "Iterative solution of nonlinear equations" , Acad. Press (1970)</TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> F.B. Hildebrand, "Introduction to numerical analysis" , Dover, reprint (1987) pp. Chapt. 8</TD></TR></table> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P. Lax, S. Burstein, A. Lax, "Calculus with applications and computing" , New York Univ. Inst. Math. Mech. (1972) {{MR|0354951}} {{ZBL|0264.26002}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.E., jr. Dennis, R. Schnable, "Least change secant updates for quasi-Newton methods" ''SIAM Review'' , '''21''' (1979) pp. 443–459 {{MR|0545880}} {{ZBL|0424.65020}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> J.M. Ortega, W.C. Rheinboldt, "Iterative solution of nonlinear equations" , Acad. Press (1970) {{MR|0273810}} {{ZBL|0241.65046}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> F.B. Hildebrand, "Introduction to numerical analysis" , Dover, reprint (1987) pp. Chapt. 8 {{MR|0895822}} {{ZBL|0641.65001}} </TD></TR></table> |
Revision as of 12:12, 27 September 2012
method of tangents
A method for the approximation of the location of the roots of a real equation
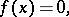 | (1) |
where 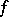 is a differentiable function. The successive approximations of Newton's method are computed by the formulas
is a differentiable function. The successive approximations of Newton's method are computed by the formulas
 | (2) |
If 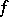 is twice continuously differentiable,
is twice continuously differentiable,  is a simple root of (1) and the initial approximation
is a simple root of (1) and the initial approximation 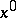 lies sufficiently close to
lies sufficiently close to 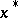 , then Newton's method has quadratic convergence, that is,
, then Newton's method has quadratic convergence, that is,
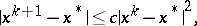 |
where  is a constant depending only on
is a constant depending only on 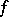 and the initial approximation
and the initial approximation 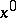 .
.
Frequently, for the solution of (1) one applies instead of (2) the so-called modified Newton method:
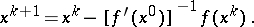 | (3) |
Under the same assumptions under which Newton's method has quadratic convergence, the method (3) has linear convergence, that is, it converges with the rate of a geometric progression with denominator less than 1.
In connection with solving a non-linear operator equation  with an operator
with an operator 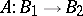 , where
, where  and
and 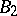 are Banach spaces, a generalization of (2) is the Newton–Kantorovich method. Its formulas are of the form
are Banach spaces, a generalization of (2) is the Newton–Kantorovich method. Its formulas are of the form
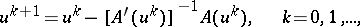 |
where  is the Fréchet derivative of
is the Fréchet derivative of 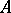 at
at  , which is an invertible operator acting from
, which is an invertible operator acting from 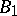 to
to  . Under special assumptions the Newton–Kantorovich method has quadratic convergence, and the corresponding modified method has linear convergence (cf. also Kantorovich process).
. Under special assumptions the Newton–Kantorovich method has quadratic convergence, and the corresponding modified method has linear convergence (cf. also Kantorovich process).
I. Newton worked out his method in 1669.
References
| [1] | L.V. Kantorovich, "Functional analysis and applied mathematics" Nat. Bur. Sci. Rep. , 1509 (1952) Uspekhi Mat. Nauk , 3 : 6 (1948) pp. 89–185 MR0053389 Zbl 0034.21203 |
| [2] | L.V. Kantorovich, G.P. Akilov, "Functionalanalysis in normierten Räumen" , Akademie Verlag (1964) (Translated from Russian) |
| [3] | L. Collatz, "Funktionalanalysis und numerische Mathematik" , Springer (1964) MR0165651 Zbl 0139.09802 |
| [4] | M.A. Krasnosel'skii, G.M. Vainikko, P.P. Zabreiko, et al., "Approximate solution of operator equations" , Wolters-Noordhoff (1972) (Translated from Russian) MR385655 Zbl 0231.41024 |
| [5] | N.S. Bakhvalov, "Numerical methods: analysis, algebra, ordinary differential equations" , MIR (1977) (Translated from Russian) MR0362811 Zbl 0524.65001 |
Comments
The Newton method is also known as the Newton–Raphson method, cf., e.g., [a4], Sect. (10.11) for single equations and Sect. (10.13) for systems of  equations.
equations.
References
| [a1] | P. Lax, S. Burstein, A. Lax, "Calculus with applications and computing" , New York Univ. Inst. Math. Mech. (1972) MR0354951 Zbl 0264.26002 |
| [a2] | J.E., jr. Dennis, R. Schnable, "Least change secant updates for quasi-Newton methods" SIAM Review , 21 (1979) pp. 443–459 MR0545880 Zbl 0424.65020 |
| [a3] | J.M. Ortega, W.C. Rheinboldt, "Iterative solution of nonlinear equations" , Acad. Press (1970) MR0273810 Zbl 0241.65046 |
| [a4] | F.B. Hildebrand, "Introduction to numerical analysis" , Dover, reprint (1987) pp. Chapt. 8 MR0895822 Zbl 0641.65001 |
Newton method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Newton_method&oldid=28253