Difference between revisions of "Motives, theory of"
(Importing text file) |
(Corrected wrong link) |
||
| Line 1: | Line 1: | ||
| − | A generalization of the various [[Cohomology|cohomology]] theories of algebraic varieties. The theory of motives systematically generalizes the idea of using the [[ | + | A generalization of the various [[Cohomology|cohomology]] theories of algebraic varieties. The theory of motives systematically generalizes the idea of using the [[Jacobi variety]] of an algebraic curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m0650401.png" /> as a replacement for the cohomology group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m0650402.png" /> in the classical theory of correspondences, and the use of this theory in the study of the [[Zeta-function|zeta-function]] of a curve <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m0650403.png" /> over a finite field. The theory of motives is universal in the sense that every geometric cohomology theory, of the type of the classical singular cohomology for algebraic varieties over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m0650404.png" /> with constant coefficients, every <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m0650405.png" />-adic cohomology theory for various prime numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m0650406.png" /> different from the characteristic of the ground field, every crystalline cohomology theory, etc. (see [[Weil cohomology|Weil cohomology]]) are functors on the category of motives. |
Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m0650407.png" /> be the category of smooth projective varieties over a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m0650408.png" /> and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m0650409.png" /> be a contravariant functor of global [[Intersection theory|intersection theory]] from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m06504010.png" /> into the category of commutative <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m06504011.png" />-algebras, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m06504012.png" /> is a fixed ring. For example, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m06504013.png" /> is the [[Chow ring|Chow ring]] of classes of algebraic cycles (cf. [[Algebraic cycle|Algebraic cycle]]) on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m06504014.png" /> modulo a suitable (rational, algebraic, numerical, etc.) equivalence relation, or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m06504015.png" /> is the Grothendieck ring, or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m06504016.png" /> is the ring of cohomology classes of even dimension, etc. The category <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m06504017.png" /> and the functor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m06504018.png" /> enable one to define a new category, the category of correspondences <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m06504019.png" />, whose objects are varieties <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m06504020.png" />, denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m06504021.png" />, and whose morphisms are defined by the formula | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m0650407.png" /> be the category of smooth projective varieties over a field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m0650408.png" /> and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m0650409.png" /> be a contravariant functor of global [[Intersection theory|intersection theory]] from <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m06504010.png" /> into the category of commutative <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m06504011.png" />-algebras, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m06504012.png" /> is a fixed ring. For example, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m06504013.png" /> is the [[Chow ring|Chow ring]] of classes of algebraic cycles (cf. [[Algebraic cycle|Algebraic cycle]]) on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m06504014.png" /> modulo a suitable (rational, algebraic, numerical, etc.) equivalence relation, or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m06504015.png" /> is the Grothendieck ring, or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m06504016.png" /> is the ring of cohomology classes of even dimension, etc. The category <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m06504017.png" /> and the functor <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m06504018.png" /> enable one to define a new category, the category of correspondences <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m06504019.png" />, whose objects are varieties <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m06504020.png" />, denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m065/m065040/m06504021.png" />, and whose morphisms are defined by the formula | ||
Revision as of 14:58, 18 September 2012
A generalization of the various cohomology theories of algebraic varieties. The theory of motives systematically generalizes the idea of using the Jacobi variety of an algebraic curve 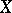 as a replacement for the cohomology group
as a replacement for the cohomology group  in the classical theory of correspondences, and the use of this theory in the study of the zeta-function of a curve
in the classical theory of correspondences, and the use of this theory in the study of the zeta-function of a curve  over a finite field. The theory of motives is universal in the sense that every geometric cohomology theory, of the type of the classical singular cohomology for algebraic varieties over
over a finite field. The theory of motives is universal in the sense that every geometric cohomology theory, of the type of the classical singular cohomology for algebraic varieties over 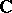 with constant coefficients, every
with constant coefficients, every  -adic cohomology theory for various prime numbers
-adic cohomology theory for various prime numbers 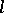 different from the characteristic of the ground field, every crystalline cohomology theory, etc. (see Weil cohomology) are functors on the category of motives.
different from the characteristic of the ground field, every crystalline cohomology theory, etc. (see Weil cohomology) are functors on the category of motives.
Let 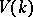 be the category of smooth projective varieties over a field
be the category of smooth projective varieties over a field  and let
and let 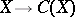 be a contravariant functor of global intersection theory from
be a contravariant functor of global intersection theory from 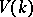 into the category of commutative
into the category of commutative 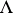 -algebras, where
-algebras, where 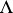 is a fixed ring. For example,
is a fixed ring. For example, 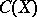 is the Chow ring of classes of algebraic cycles (cf. Algebraic cycle) on
is the Chow ring of classes of algebraic cycles (cf. Algebraic cycle) on  modulo a suitable (rational, algebraic, numerical, etc.) equivalence relation, or
modulo a suitable (rational, algebraic, numerical, etc.) equivalence relation, or 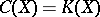 is the Grothendieck ring, or
is the Grothendieck ring, or 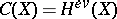 is the ring of cohomology classes of even dimension, etc. The category
is the ring of cohomology classes of even dimension, etc. The category 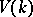 and the functor
and the functor 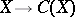 enable one to define a new category, the category of correspondences
enable one to define a new category, the category of correspondences 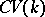 , whose objects are varieties
, whose objects are varieties 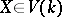 , denoted by
, denoted by 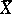 , and whose morphisms are defined by the formula
, and whose morphisms are defined by the formula
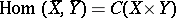 |
with the usual composition law for correspondences (see [1]). Let the functor 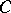 take values in the category of commutative graded
take values in the category of commutative graded 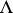 -algebras
-algebras 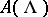 . Then
. Then 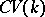 will be the
will be the  -additive category of graded correspondences. Moreover,
-additive category of graded correspondences. Moreover, 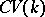 will have direct sums and tensor products.
will have direct sums and tensor products.
The category whose objects are the varieties from 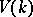 and whose morphisms are correspondences of degree
and whose morphisms are correspondences of degree  is denoted by
is denoted by 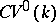 . A natural functor from
. A natural functor from 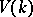 into
into 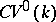 has been defined, and the functor
has been defined, and the functor 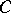 extends to a functor
extends to a functor 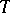 from
from 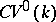 to
to 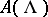 . The category
. The category 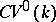 , like
, like 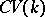 , is not Abelian. Its pseudo-Abelian completion, the category
, is not Abelian. Its pseudo-Abelian completion, the category 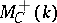 , has been considered. It is obtained from
, has been considered. It is obtained from 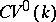 by the formal addition of the images of all projections
by the formal addition of the images of all projections 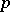 . More precisely, the objects of
. More precisely, the objects of  are pairs
are pairs 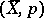 , where
, where 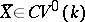 and
and 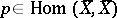 ,
, 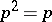 , and
, and 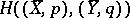 is the set of correspondences
is the set of correspondences 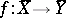 such that
such that 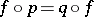 modulo a correspondence
modulo a correspondence 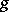 with
with 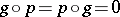 . The category
. The category 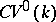 is imbedded in
is imbedded in 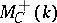 by means of the functor
by means of the functor 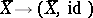 . The natural functor
. The natural functor 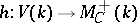 is called the functor of motive cohomology spaces and
is called the functor of motive cohomology spaces and 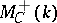 is called the category of effective motives.
is called the category of effective motives.
Let 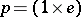 , where
, where  is the class of any rational point on the projective line
is the class of any rational point on the projective line 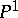 , and let
, and let  . Then
. Then
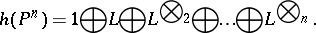 |
If 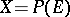 is the projectivization of a locally free sheaf
is the projectivization of a locally free sheaf 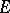 of rank
of rank  on
on 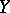 , then
, then
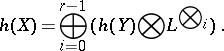 |
Motives of a monodial transformation with a non-singular centre, motives of curves (see [1]), motives of Abelian manifolds (see [2]), and motives of Weil hypersurfaces have also been calculated.
The category of motives 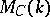 is obtained from
is obtained from 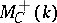 by the formal addition of negative powers of the motives
by the formal addition of negative powers of the motives 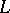 . By analogy with
. By analogy with 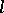 -adic cohomology,
-adic cohomology, 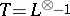 is called the Tate motive. Tensor multiplication with
is called the Tate motive. Tensor multiplication with 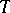 is called twisting by the Tate motive. Twisting enables one to define the level of a motive as in an
is called twisting by the Tate motive. Twisting enables one to define the level of a motive as in an 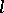 -adic cohomology theory. Any functor of the Weil cohomology factors through the functor
-adic cohomology theory. Any functor of the Weil cohomology factors through the functor 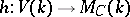 . There is the conjecture that
. There is the conjecture that 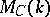 does not, in some sense, depend on the intersection theory of
does not, in some sense, depend on the intersection theory of 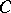 , and that the functor
, and that the functor 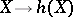 is itself a (universal) theory for the Weil cohomology. This conjecture is closely related to the standard Grothendieck conjectures (see [5]) on algebraic cycles (at present, 1982, not proved).
is itself a (universal) theory for the Weil cohomology. This conjecture is closely related to the standard Grothendieck conjectures (see [5]) on algebraic cycles (at present, 1982, not proved).
References
| [1] | Yu.I. Manin, "Correspondences, motives and monoidal transformations" Math. USSR Sb. , 6 : 4 (1968) pp. 439–470 Mat. Sb. , 77 : 4 (1968) pp. 475–507 |
| [2] | A.M. Shermenev, "The motif of an abelian variety" Uspekhi Mat. Nauk , 26 : 2 (1971) pp. 215–216 (In Russian) |
| [3] | M. Demazure, "Motives des variétés algébrique" , Sem. Bourbaki Exp. 365 , Lect. notes in math. , 180 , Springer (1971) pp. 19–38 |
| [4] | S.L. Kleiman, "Motives" P. Holm (ed.) , Algebraic Geom. Proc. 5-th Nordic Summer School Math. Oslo, 1970 , Wolters-Noordhoff (1972) pp. 53–96 |
| [5] | S.L. Kleiman, "Algebraic cycles and the Weil conjectures" A. Grothendieck (ed.) J. Giraud (ed.) et al. (ed.) , Dix exposés sur la cohomologie des schémas , North-Holland & Masson (1968) pp. 359–386 |
Comments
The theory of motives has been created by A. Grothendieck in the 1960-s. Although the above-mentioned standard conjectures on algebraic cycles have not yet (1989) been proved, the theory of motives has played an important role in various recent developments, for instance: i) as a guide for the Deligne–Hodge theory ([a1]); ii) in the study of absolute Hodge cycles on Abelian varieties ([a2]), where a variant of the notion of a motive has been used; iii) in the study of Chow groups on certain varieties over a finite field ([a3]); and iv) in work on the Beilinson's conjectures on special values of 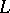 -functions (see [a4]).
-functions (see [a4]).
References
| [a1] | P. Deligne, "Theory de Hodge I" , Proc. Internat. Congress Mathematicians (Nice, 1970) , 1 , Gauthier-Villars (1971) pp. 425–430 |
| [a2] | P. Deligne (ed.) J.S. Milne (ed.) A. Ogus (ed.) K. Shih (ed.) , Hodge cycles, motives and Shimura varieties , Lect. notes in math. , 900 , Springer (1980) |
| [a3] | C. Soulé, "Groupes de Chow et 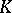 -theory des variétés sur un corps fini" Math. Ann. , 268 (1984) pp. 317–345 -theory des variétés sur un corps fini" Math. Ann. , 268 (1984) pp. 317–345 |
| [a4] | M. Rapoport (ed.) N. Schappacher (ed.) P. Schneider (ed.) , Beilinson's conjectures on special values of 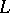 -functions , Acad. Press (1988) -functions , Acad. Press (1988) |
Motives, theory of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Motives,_theory_of&oldid=28019