Difference between revisions of "Von Neumann ergodic theorem"
From Encyclopedia of Mathematics
(MSC|47A35 Category:General theory of linear operators) |
(refs format) |
||
| Line 13: | Line 13: | ||
exists (in the same sense). Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691010.png" /> is the orthogonal projection of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691011.png" /> onto the space of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691012.png" />- (or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691013.png" />-) invariant elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691014.png" />. | exists (in the same sense). Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691010.png" /> is the orthogonal projection of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691011.png" /> onto the space of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691012.png" />- (or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691013.png" />-) invariant elements of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691014.png" />. | ||
| − | J. von Neumann stated and proved this theorem in | + | J. von Neumann stated and proved this theorem in {{Cite|N}}, having in mind in the first instance its application in ergodic theory, when in a [[Measure space|measure space]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691015.png" /> an endomorphism <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691016.png" /> is given (or a [[Measurable flow|measurable flow]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691017.png" />), when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691018.png" /> and where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691019.png" /> is the shift operator: |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691020.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691020.png" /></td> </tr></table> | ||
| Line 19: | Line 19: | ||
In this case von Neumann's theorem states that the time average of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691021.png" />, that is, the mean value of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691022.png" />, or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691023.png" />, on the time interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691024.png" />, or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691025.png" />, when this interval is lengthened, converges to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691026.png" /> in mean square with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691027.png" /> (which is often emphasized by the term mean ergodic theorem). In particular, for a sufficiently long interval the averaged time mean of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691028.png" /> for the majority of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691029.png" /> is close to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691030.png" />. Therefore, von Neumann's theorem (and its generalizations) is frequently (especially when applied to a given case) called the statistical ergodic theorem, in contrast to the individual ergodic theorem, that is, the [[Birkhoff ergodic theorem|Birkhoff ergodic theorem]] (and its generalizations). From the latter (and for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691031.png" />, from arguments used in its proof) one can in this case deduce von Neumann's ergodic theorem. However, in general, when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691032.png" /> is not realized as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691033.png" /> and the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691034.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691035.png" /> is not connected with any transformation in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691036.png" />, von Neumann's theorem does not follow from Birkhoff's. | In this case von Neumann's theorem states that the time average of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691021.png" />, that is, the mean value of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691022.png" />, or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691023.png" />, on the time interval <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691024.png" />, or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691025.png" />, when this interval is lengthened, converges to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691026.png" /> in mean square with respect to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691027.png" /> (which is often emphasized by the term mean ergodic theorem). In particular, for a sufficiently long interval the averaged time mean of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691028.png" /> for the majority of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691029.png" /> is close to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691030.png" />. Therefore, von Neumann's theorem (and its generalizations) is frequently (especially when applied to a given case) called the statistical ergodic theorem, in contrast to the individual ergodic theorem, that is, the [[Birkhoff ergodic theorem|Birkhoff ergodic theorem]] (and its generalizations). From the latter (and for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691031.png" />, from arguments used in its proof) one can in this case deduce von Neumann's ergodic theorem. However, in general, when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691032.png" /> is not realized as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691033.png" /> and the operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691034.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691035.png" /> is not connected with any transformation in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/v/v096/v096910/v09691036.png" />, von Neumann's theorem does not follow from Birkhoff's. | ||
| − | Von Neumann's original proof was based on the spectral decomposition of unitary operators. Later a number of other proofs were published (the simplest is due to F. Riesz, see | + | Von Neumann's original proof was based on the spectral decomposition of unitary operators. Later a number of other proofs were published (the simplest is due to F. Riesz, see {{Cite|H}}) and it was generalized to wider classes of groups and semi-groups of operators on Banach spaces (see {{Cite|VY}}, {{Cite|KSS}}). |
Von Neumann's theorem, and its generalizations, is an [[Operator ergodic theorem|operator ergodic theorem]]. | Von Neumann's theorem, and its generalizations, is an [[Operator ergodic theorem|operator ergodic theorem]]. | ||
====References==== | ====References==== | ||
| − | + | {| | |
| − | + | |valign="top"|{{Ref|N}}|| J. von Neumann, "Proof of the quasi-ergodic hypothesis" ''Proc. Nat. Acad. Sci. USA'' , '''18''' (1932) pp. 70–82 {{MR|}} {{ZBL|0004.31004}} {{ZBL|58.1271.03}} | |
| − | + | |- | |
| + | |valign="top"|{{Ref|H}}|| P.R. Halmos, "Lectures on ergodic theory" , Math. Soc. Japan (1956) {{MR|0097489}} {{ZBL|0073.09302}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|VY}}|| A.M. Vershik, S.A. Yuzvinskii, "Dynamical systems with an invariant measure" ''Progress in Math.'' , '''8''' (1970) pp. 151–215 ''Itogi Nauk. Mat. Anal. 1967'' (1969) pp. 133–187 {{MR|286981}} {{ZBL|}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|KSS}}|| A.B. Katok, Ya.G. Sinai, A.M. Stepin, "Theory of dynamical systems and general transformation groups with invariant measure" ''J. Soviet Math.'' , '''7''' : 6 (1977) pp. 964–1065 ''Itogi Nauk. i Tekhn. Mat. Anal.'' , '''13''' (1975) pp. 129–262 {{MR|0584389}} {{ZBL|0399.28011}} | ||
| + | |} | ||
====Comments==== | ====Comments==== | ||
| − | For a wider variety of ergodic theorems see | + | For a wider variety of ergodic theorems see {{Cite|K}}. |
====References==== | ====References==== | ||
| − | + | {| | |
| + | |valign="top"|{{Ref|K}}|| U. Krengel, "Ergodic theorems" , de Gruyter (1985) {{MR|0797411}} {{ZBL|0575.28009}} | ||
| + | |} | ||
Revision as of 19:01, 2 June 2012
2020 Mathematics Subject Classification: Primary: 47A35 [MSN][ZBL]
For any isometric operator 
on a Hilbert space 
and for any 
the limit
 |
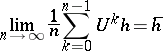exists (in the sense of convergence in the norm of 
). For a continuous one-parameter group of unitary transformations 
on 
and any 
, the limit
 |
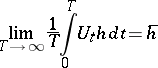exists (in the same sense). Here 
is the orthogonal projection of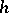 
onto the space of 
- (or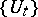 
-) invariant elements of 
.
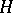J. von Neumann stated and proved this theorem in [N], having in mind in the first instance its application in ergodic theory, when in a measure space 
an endomorphism 
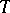is given (or a measurable flow 
), when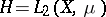 
and where 
is the shift operator:
 |
In this case von Neumann's theorem states that the time average of 
, that is, the mean value of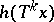 
, or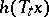 
, on the time interval 
, or 
, when this interval is lengthened, converges to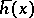 
in mean square with respect to 
(which is often emphasized by the term mean ergodic theorem). In particular, for a sufficiently long interval the averaged time mean of 
for the majority of 
is close to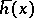 
. Therefore, von Neumann's theorem (and its generalizations) is frequently (especially when applied to a given case) called the statistical ergodic theorem, in contrast to the individual ergodic theorem, that is, the Birkhoff ergodic theorem (and its generalizations). From the latter (and for 
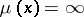, from arguments used in its proof) one can in this case deduce von Neumann's ergodic theorem. However, in general, when 
is not realized as 
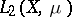and the operator 
or 
is not connected with any transformation in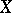 
, von Neumann's theorem does not follow from Birkhoff's.
Von Neumann's original proof was based on the spectral decomposition of unitary operators. Later a number of other proofs were published (the simplest is due to F. Riesz, see [H]) and it was generalized to wider classes of groups and semi-groups of operators on Banach spaces (see [VY], [KSS]).
Von Neumann's theorem, and its generalizations, is an operator ergodic theorem.
References
| [N] | J. von Neumann, "Proof of the quasi-ergodic hypothesis" Proc. Nat. Acad. Sci. USA , 18 (1932) pp. 70–82 Zbl 0004.31004 Zbl 58.1271.03 |
| [H] | P.R. Halmos, "Lectures on ergodic theory" , Math. Soc. Japan (1956) MR0097489 Zbl 0073.09302 |
| [VY] | A.M. Vershik, S.A. Yuzvinskii, "Dynamical systems with an invariant measure" Progress in Math. , 8 (1970) pp. 151–215 Itogi Nauk. Mat. Anal. 1967 (1969) pp. 133–187 MR286981 |
| [KSS] | A.B. Katok, Ya.G. Sinai, A.M. Stepin, "Theory of dynamical systems and general transformation groups with invariant measure" J. Soviet Math. , 7 : 6 (1977) pp. 964–1065 Itogi Nauk. i Tekhn. Mat. Anal. , 13 (1975) pp. 129–262 MR0584389 Zbl 0399.28011 |
Comments
For a wider variety of ergodic theorems see [K].
References
| [K] | U. Krengel, "Ergodic theorems" , de Gruyter (1985) MR0797411 Zbl 0575.28009 |
How to Cite This Entry:
Von Neumann ergodic theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Von_Neumann_ergodic_theorem&oldid=26972
Von Neumann ergodic theorem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Von_Neumann_ergodic_theorem&oldid=26972
This article was adapted from an original article by D.V. Anosov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article