Difference between revisions of "Transition-operator semi-group"
(MSC|60J35|47D07 Category:Markov processes) |
(refs format) |
||
| Line 3: | Line 3: | ||
[[Category:Markov processes]] | [[Category:Markov processes]] | ||
| − | The [[Semi-group of operators|semi-group of operators]] generated by the [[Transition function|transition function]] of a [[Markov process|Markov process]]. From the transition function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t0937701.png" /> of a homogeneous Markov process <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t0937702.png" /> in a state space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t0937703.png" /> one can construct certain semi-groups of linear operators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t0937704.png" /> acting in some Banach space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t0937705.png" /> | + | The [[Semi-group of operators|semi-group of operators]] generated by the [[Transition function|transition function]] of a [[Markov process|Markov process]]. From the transition function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t0937701.png" /> of a homogeneous Markov process <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t0937702.png" /> in a state space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t0937703.png" /> one can construct certain semi-groups of linear operators <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t0937704.png" /> acting in some Banach space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t0937705.png" /> {{Cite|F}}. Very often, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t0937706.png" /> is the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t0937707.png" /> of bounded real-valued measurable functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t0937708.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t0937709.png" /> with the uniform norm (or for a [[Feller process|Feller process]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377010.png" />, the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377011.png" /> of continuous functions with the same norm) or else the space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377012.png" /> of finite countably-additive functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377013.png" /> on <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377014.png" /> with the complete variation as norm. In the first two cases one puts |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377015.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377015.png" /></td> </tr></table> | ||
| Line 27: | Line 27: | ||
(for this reason, in particular, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377043.png" /> is called the potential of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377044.png" />). | (for this reason, in particular, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377043.png" /> is called the potential of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377044.png" />). | ||
| − | Knowledge of the infinitesimal generator enables one to derive important characteristics of the initial process; the classification of Markov processes amounts to the description of their corresponding infinitesimal generators | + | Knowledge of the infinitesimal generator enables one to derive important characteristics of the initial process; the classification of Markov processes amounts to the description of their corresponding infinitesimal generators {{Cite|Dy}}, {{Cite|GS}}. Also, using the infinitesimal generator one can find the mean values of various functionals. For example, under certain assumptions the function |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377045.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377045.png" /></td> </tr></table> | ||
| Line 33: | Line 33: | ||
is a unique solution to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377046.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377047.png" />, which is a not-too-rapidly-increasing function of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377048.png" />. Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377049.png" /> is the mathematical expectation corresponding to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377050.png" />, while <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377051.png" />. | is a unique solution to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377046.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377047.png" />, which is a not-too-rapidly-increasing function of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377048.png" />. Here <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377049.png" /> is the mathematical expectation corresponding to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377050.png" />, while <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377051.png" />. | ||
| − | The operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377052.png" /> is related to the characteristic operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377053.png" /> | + | The operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377052.png" /> is related to the characteristic operator <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377053.png" /> {{Cite|Dy}}. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377054.png" /> be a Markov process that is right continuous in a topological space <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377055.png" />. For a Borel function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377056.png" /> one puts |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377057.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/t/t093/t093770/t09377057.png" /></td> </tr></table> | ||
| Line 40: | Line 40: | ||
====References==== | ====References==== | ||
| − | + | {| | |
| − | + | |valign="top"|{{Ref|F}}|| W. Feller, "The parabolic differential equations and the associated semi-groups of transformations" ''Ann. of Math.'' , '''55''' (1952) pp. 468–519 {{MR|0047886}} {{ZBL|}} | |
| − | + | |- | |
| + | |valign="top"|{{Ref|Dy}}|| E.B. Dynkin, "Foundations of the theory of Markov processes" , Springer (1961) (Translated from Russian) {{MR|0131898}} {{ZBL|}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|GS}}|| I.I. Gihman, A.V. Skorohod, "The theory of stochastic processes" , '''2''' , Springer (1975) (Translated from Russian) {{MR|0375463}} {{ZBL|0305.60027}} | ||
| + | |} | ||
====Comments==== | ====Comments==== | ||
| Line 48: | Line 52: | ||
====References==== | ====References==== | ||
| − | + | {| | |
| + | |valign="top"|{{Ref|BG}}|| R.M. Blumenthal, R.K. Getoor, "Markov processes and potential theory" , Acad. Press (1968) {{MR|0264757}} {{ZBL|0169.49204}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|Do}}|| J.L. Doob, "Classical potential theory and its probabilistic counterpart" , Springer (1984) pp. 390 {{MR|0731258}} {{ZBL|0549.31001}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|Dy2}}|| E.B. Dynkin, "Markov processes" , '''1''' , Springer (1965) (Translated from Russian) {{MR|0193671}} {{ZBL|0132.37901}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|F2}}|| W. Feller, "An introduction to probability theory and its applications" , '''1–2''' , Wiley (1966) {{MR|0210154}} {{ZBL|0138.10207}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|L}}|| M. Loève, "Probability theory" , '''II''' , Springer (1978) {{MR|0651017}} {{MR|0651018}} {{ZBL|0385.60001}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|DM}}|| C. Dellacherie, P.A. Meyer, "Probabilities and potential" , '''1–3''' , North-Holland (1978–1988) pp. Chapts. XII-XVI (Translated from French) {{MR|0939365}} {{MR|0898005}} {{MR|0727641}} {{MR|0745449}} {{MR|0566768}} {{MR|0521810}} {{ZBL|0716.60001}} {{ZBL|0494.60002}} {{ZBL|0494.60001}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|S}}|| M.J. Sharpe, "General theory of Markov processes" , Acad. Press (1988) {{MR|0958914}} {{ZBL|0649.60079}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|AM}}|| S. Albeverio, Zh.M. Ma, "A note on quasicontinuous kernels representing quasilinear positive maps" ''Forum Math.'' , '''3''' (1991) pp. 389–400 | ||
| + | |} | ||
Revision as of 14:16, 31 May 2012
2020 Mathematics Subject Classification: Primary: 60J35 Secondary: 47D07 [MSN][ZBL]
The semi-group of operators generated by the transition function of a Markov process. From the transition function 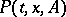 of a homogeneous Markov process
of a homogeneous Markov process 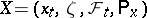 in a state space
in a state space 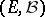 one can construct certain semi-groups of linear operators
one can construct certain semi-groups of linear operators 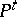 acting in some Banach space
acting in some Banach space 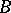 [F]. Very often,
[F]. Very often, 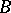 is the space
is the space 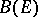 of bounded real-valued measurable functions
of bounded real-valued measurable functions 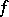 in
in 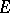 with the uniform norm (or for a Feller process
with the uniform norm (or for a Feller process 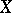 , the space
, the space 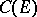 of continuous functions with the same norm) or else the space
of continuous functions with the same norm) or else the space 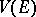 of finite countably-additive functions
of finite countably-additive functions 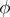 on
on 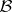 with the complete variation as norm. In the first two cases one puts
with the complete variation as norm. In the first two cases one puts
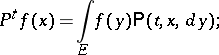 |
and in the third
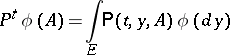 |
(here 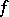 and
and 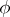 belong to the corresponding spaces,
belong to the corresponding spaces, 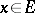 ,
, 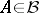 ). In all these cases the semi-group property holds:
). In all these cases the semi-group property holds: 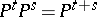 ,
, 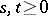 , and any of the three semi-groups
, and any of the three semi-groups 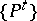 is called a transition-operator semi-group.
is called a transition-operator semi-group.
In what follows, only the first case is considered. The usual definition of the infinitesimal generator 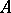 of the semi-group
of the semi-group 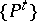 (this is also the infinitesimal generator of the process) is as follows:
(this is also the infinitesimal generator of the process) is as follows:
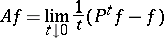 |
for all 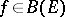 for which this limit exists as a limit in
for which this limit exists as a limit in 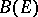 . It is assumed that
. It is assumed that 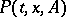 for
for 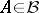 is a measurable function of the pair of variables
is a measurable function of the pair of variables 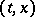 , and one introduces the resolvent
, and one introduces the resolvent 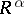 of the process
of the process 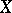 ,
,  , by:
, by:
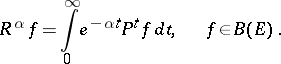 | (*) |
If 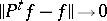 as
as 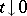 , then
, then 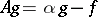 , where
, where 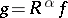 . Under certain assumptions the integral (*) exists also for
. Under certain assumptions the integral (*) exists also for 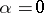 , and
, and 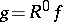 satisfies the "Poisson equation"
satisfies the "Poisson equation"
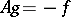 |
(for this reason, in particular, 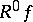 is called the potential of
is called the potential of 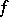 ).
).
Knowledge of the infinitesimal generator enables one to derive important characteristics of the initial process; the classification of Markov processes amounts to the description of their corresponding infinitesimal generators [Dy], [GS]. Also, using the infinitesimal generator one can find the mean values of various functionals. For example, under certain assumptions the function
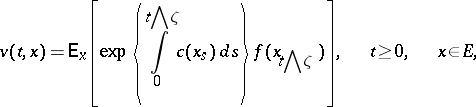 |
is a unique solution to 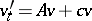 ,
, 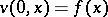 , which is a not-too-rapidly-increasing function of
, which is a not-too-rapidly-increasing function of 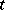 . Here
. Here 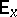 is the mathematical expectation corresponding to
is the mathematical expectation corresponding to 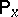 , while
, while 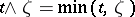 .
.
The operator 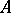 is related to the characteristic operator
is related to the characteristic operator 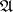 [Dy]. Let
[Dy]. Let 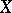 be a Markov process that is right continuous in a topological space
be a Markov process that is right continuous in a topological space 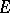 . For a Borel function
. For a Borel function 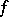 one puts
one puts
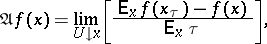 |
if the limit exists for all 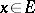 , where
, where 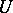 runs through a system of neighbourhoods of the point
runs through a system of neighbourhoods of the point  contracting towards
contracting towards  and where
and where  is the moment of first exit of
is the moment of first exit of 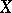 from
from 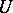 (if
(if 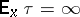 , the fraction in the limit is set equal to zero). In many cases the calculation of
, the fraction in the limit is set equal to zero). In many cases the calculation of 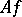 amounts to calculating
amounts to calculating 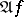 .
.
References
| [F] | W. Feller, "The parabolic differential equations and the associated semi-groups of transformations" Ann. of Math. , 55 (1952) pp. 468–519 MR0047886 |
| [Dy] | E.B. Dynkin, "Foundations of the theory of Markov processes" , Springer (1961) (Translated from Russian) MR0131898 |
| [GS] | I.I. Gihman, A.V. Skorohod, "The theory of stochastic processes" , 2 , Springer (1975) (Translated from Russian) MR0375463 Zbl 0305.60027 |
Comments
References
| [BG] | R.M. Blumenthal, R.K. Getoor, "Markov processes and potential theory" , Acad. Press (1968) MR0264757 Zbl 0169.49204 |
| [Do] | J.L. Doob, "Classical potential theory and its probabilistic counterpart" , Springer (1984) pp. 390 MR0731258 Zbl 0549.31001 |
| [Dy2] | E.B. Dynkin, "Markov processes" , 1 , Springer (1965) (Translated from Russian) MR0193671 Zbl 0132.37901 |
| [F2] | W. Feller, "An introduction to probability theory and its applications" , 1–2 , Wiley (1966) MR0210154 Zbl 0138.10207 |
| [L] | M. Loève, "Probability theory" , II , Springer (1978) MR0651017 MR0651018 Zbl 0385.60001 |
| [DM] | C. Dellacherie, P.A. Meyer, "Probabilities and potential" , 1–3 , North-Holland (1978–1988) pp. Chapts. XII-XVI (Translated from French) MR0939365 MR0898005 MR0727641 MR0745449 MR0566768 MR0521810 Zbl 0716.60001 Zbl 0494.60002 Zbl 0494.60001 |
| [S] | M.J. Sharpe, "General theory of Markov processes" , Acad. Press (1988) MR0958914 Zbl 0649.60079 |
| [AM] | S. Albeverio, Zh.M. Ma, "A note on quasicontinuous kernels representing quasilinear positive maps" Forum Math. , 3 (1991) pp. 389–400 |
Transition-operator semi-group. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Transition-operator_semi-group&oldid=26962