Difference between revisions of "Stochastic equivalence"
(MSC|60Gxx|60Axx) |
(refs format) |
||
| Line 11: | Line 11: | ||
====References==== | ====References==== | ||
| − | + | {| | |
| + | |valign="top"|{{Ref|Do}}|| J.L. Doob, "Classical potential theory and its probabilistic counterpart" , Springer (1984) pp. 390 {{MR|0731258}} {{ZBL|0549.31001}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|GS}}|| I.I. Gihman, A.V. Skorohod, "The theory of stochastic processes" , '''1''' , Springer (1974) pp. 43ff (Translated from Russian) {{MR|0346882}} {{ZBL|0291.60019}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|De}}|| C. Dellacherie, "Capacités et processus stochastiques" , Springer (1972) pp. 46 {{MR|0448504}} {{ZBL|0246.60032}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|S}}|| A.V. Skorohod, "Random processes with independent increments" , Kluwer (1991) pp. 9 (Translated from Russian) {{MR|1155400}} {{ZBL|}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|LS}}|| R.Sh. Liptser, A.N. Shiryayev, "Theory of martingales" , Kluwer (1989) pp. 4 (Translated from Russian) {{MR|1022664}} {{ZBL|0728.60048}} | ||
| + | |} | ||
Revision as of 17:50, 29 May 2012
2020 Mathematics Subject Classification: Primary: 60Gxx Secondary: 60Axx [MSN][ZBL]
The equivalence relation between random variables that differ only on a set of probability zero. More precisely, two random variables  and
and 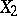 , defined on a common probability space
, defined on a common probability space  , are called stochastically equivalent if
, are called stochastically equivalent if  . In most problems of probability theory one deals with classes of equivalent random variables, rather than with the random variables themselves.
. In most problems of probability theory one deals with classes of equivalent random variables, rather than with the random variables themselves.
Two stochastic processes  and
and  ,
,  , defined on a common probability space are called stochastically equivalent if for any
, defined on a common probability space are called stochastically equivalent if for any  stochastic equivalence holds between the corresponding random variables:
stochastic equivalence holds between the corresponding random variables:  . With regard to stochastic processes
. With regard to stochastic processes 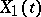 and
and 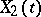 with coinciding finite-dimensional distributions, the term "stochastic equivalence" is sometimes used in the broad sense.
with coinciding finite-dimensional distributions, the term "stochastic equivalence" is sometimes used in the broad sense.
Comments
The members of a stochastic equivalence class (of random variables or stochastic processes) are sometimes referred to as versions (of each other or of the equivalence class). A version of a random variable or stochastic process is also called a modification.
References
| [Do] | J.L. Doob, "Classical potential theory and its probabilistic counterpart" , Springer (1984) pp. 390 MR0731258 Zbl 0549.31001 |
| [GS] | I.I. Gihman, A.V. Skorohod, "The theory of stochastic processes" , 1 , Springer (1974) pp. 43ff (Translated from Russian) MR0346882 Zbl 0291.60019 |
| [De] | C. Dellacherie, "Capacités et processus stochastiques" , Springer (1972) pp. 46 MR0448504 Zbl 0246.60032 |
| [S] | A.V. Skorohod, "Random processes with independent increments" , Kluwer (1991) pp. 9 (Translated from Russian) MR1155400 |
| [LS] | R.Sh. Liptser, A.N. Shiryayev, "Theory of martingales" , Kluwer (1989) pp. 4 (Translated from Russian) MR1022664 Zbl 0728.60048 |
Stochastic equivalence. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Stochastic_equivalence&oldid=26950