Difference between revisions of "Multinomial distribution"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
(refs format) |
||
| Line 30: | Line 30: | ||
====References==== | ====References==== | ||
| − | + | {| | |
| − | + | |valign="top"|{{Ref|C}}|| H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) {{MR|0016588}} {{ZBL|0063.01014}} | |
| − | + | |} | |
====Comments==== | ====Comments==== | ||
| Line 38: | Line 38: | ||
====References==== | ====References==== | ||
| − | + | {| | |
| + | |valign="top"|{{Ref|JK}}|| N.L. Johnson, S. Kotz, "Discrete distributions" , Wiley (1969) {{MR|0268996}} {{ZBL|0292.62009}} | ||
| + | |} | ||
Revision as of 06:04, 15 May 2012
polynomial distribution
2020 Mathematics Subject Classification: Primary: 60E99 [MSN][ZBL]
The joint distribution of random variables  that is defined for any set of non-negative integers
that is defined for any set of non-negative integers  satisfying the condition
satisfying the condition  ,
,  ,
,  , by the formula
, by the formula
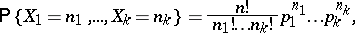 | (*) |
where  (
( ,
,  ) are the parameters of the distribution. A multinomial distribution is a multivariate discrete distribution, namely the distribution for the random vector
) are the parameters of the distribution. A multinomial distribution is a multivariate discrete distribution, namely the distribution for the random vector 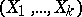 with
with 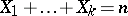 (this distribution is in essence
(this distribution is in essence 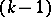 -dimensional, since it is degenerate in the Euclidean space of
-dimensional, since it is degenerate in the Euclidean space of 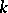 dimensions). A multinomial distribution is a natural generalization of a binomial distribution and coincides with the latter for
dimensions). A multinomial distribution is a natural generalization of a binomial distribution and coincides with the latter for 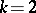 . The name of the distribution is given because the probability (*) is the general term in the expansion of the multinomial
. The name of the distribution is given because the probability (*) is the general term in the expansion of the multinomial 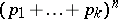 . The multinomial distribution appears in the following probability scheme. Each of the random variables
. The multinomial distribution appears in the following probability scheme. Each of the random variables  is the number of occurrences of one of the mutually exclusive events
is the number of occurrences of one of the mutually exclusive events 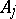 ,
, 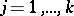 , in repeated independent trials. If in each trial the probability of event
, in repeated independent trials. If in each trial the probability of event  is
is  ,
,  , then the probability (*) is equal to the probability that in
, then the probability (*) is equal to the probability that in  trials the events
trials the events  will appear
will appear  times, respectively. Each of the random variables
times, respectively. Each of the random variables 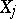 has a binomial distribution with mathematical expectation
has a binomial distribution with mathematical expectation 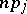 and variance
and variance  .
.
The random vector 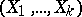 has mathematical expectation
has mathematical expectation 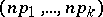 and covariance matrix
and covariance matrix 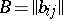 , where
, where
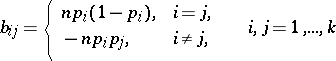 |
(the rank of the matrix 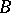 is
is  because
because 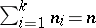 ). The characteristic function of a multinomial distribution is
). The characteristic function of a multinomial distribution is
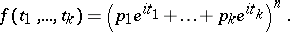 |
For 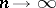 , the distribution of the vector
, the distribution of the vector  with normalized components
with normalized components
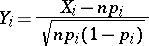 |
tends to a certain multivariate normal distribution, while the distribution of the sum
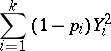 |
(which is used in mathematical statistics to construct the "chi-squared" test) tends to the "chi-squared" distribution with  degrees of freedom.
degrees of freedom.
References
| [C] | H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) MR0016588 Zbl 0063.01014 |
Comments
References
| [JK] | N.L. Johnson, S. Kotz, "Discrete distributions" , Wiley (1969) MR0268996 Zbl 0292.62009 |
Multinomial distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Multinomial_distribution&oldid=26633