Difference between revisions of "Functional of a Markov process"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
(refs format) |
||
| Line 18: | Line 18: | ||
====References==== | ====References==== | ||
| − | + | {| | |
| − | + | |valign="top"|{{Ref|LS}}|| R.S. Liptser, A.N. Shiryaev, "Statistics of random processes" , '''1–2''' , Springer (1977–1978) (Translated from Russian) {{MR|1800858}} {{MR|1800857}} {{MR|0608221}} {{MR|0488267}} {{MR|0474486}} {{ZBL|1008.62073}} {{ZBL|1008.62072}} {{ZBL|0556.60003}} {{ZBL|0369.60001}} {{ZBL|0364.60004}} | |
| − | + | |- | |
| + | |valign="top"|{{Ref|D}}|| E.B. Dynkin, "Foundations of the theory of Markov processes" , Springer (1961) (Translated from Russian) {{MR|0131898}} {{ZBL|}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|D2}}|| E.B. Dynkin, "Markov processes" , '''1–2''' , Springer (1965) (Translated from Russian) {{MR|0193671}} {{ZBL|0132.37901}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|R}}|| D. Revuz, "Mesures associees aux fonctionelles additive de Markov I" ''Trans. Amer. Math. Soc.'' , '''148''' (1970) pp. 501–531 | ||
| + | |- | ||
| + | |valign="top"|{{Ref|B}}|| A. Benveniste, "Application de deux théorèmes de G. Mokobodzki à l'étude du noyau de Lévy d'un processus de Hunt sans hypothèse (L)" , ''Lect. notes in math.'' , '''321''' , Springer (1973) pp. 1–24 {{MR|0415781}} {{MR|0415782}} {{ZBL|}} | ||
| + | |} | ||
====Comments==== | ====Comments==== | ||
The trace of an algebra of sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042080/f04208079.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042080/f04208080.png" /> with respect to a subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042080/f04208081.png" /> is the algebra of sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042080/f04208082.png" />. It is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042080/f04208083.png" />-algebra if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042080/f04208084.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042080/f04208085.png" />-algebra. | The trace of an algebra of sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042080/f04208079.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042080/f04208080.png" /> with respect to a subset <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042080/f04208081.png" /> is the algebra of sets <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042080/f04208082.png" />. It is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042080/f04208083.png" />-algebra if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042080/f04208084.png" /> is a <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/f/f042/f042080/f04208085.png" />-algebra. | ||
Revision as of 06:29, 13 May 2012
2020 Mathematics Subject Classification: Primary: 60Jxx Secondary: 60J5560J57 [MSN][ZBL]
A random variable or random function depending in a measurable way on the trajectory of the Markov process; the condition of measurability varies according to the concrete situation. In the general theory of Markov processes one takes the following definition of a functional. Suppose that a non-stopped homogeneous Markov process 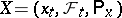 with time shift operators
with time shift operators 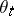 is given on a measurable space
is given on a measurable space 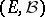 , let
, let 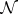 be the smallest
be the smallest 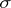 -algebra in the space of elementary events containing every event of the form
-algebra in the space of elementary events containing every event of the form 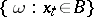 , where
, where 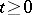 ,
, 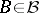 , and let
, and let 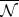 be the intersection of all completions of
be the intersection of all completions of 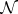 by all possible measures
by all possible measures 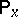 (
(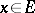 ). A random function
). A random function  ,
, 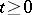 , is called a functional of the Markov process
, is called a functional of the Markov process 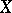 if, for every
if, for every 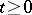 ,
, 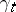 is measurable relative to the
is measurable relative to the 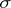 -algebra
-algebra 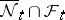 .
.
Of particular interest are multiplicative and additive functionals of Markov processes. The first of these are distinguished by the condition 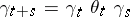 , and the second by the condition
, and the second by the condition 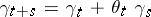 ,
, 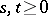 , where
, where 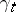 is assumed to be continuous on the right on
is assumed to be continuous on the right on 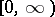 (on the other hand, it is sometimes appropriate to assume that these conditions are satisfied only
(on the other hand, it is sometimes appropriate to assume that these conditions are satisfied only 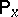 -almost certainly for all fixed
-almost certainly for all fixed 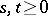 ). One takes analogous formulations in the case of stopped and inhomogeneous processes. One can obtain examples of additive functionals of a Markov process
). One takes analogous formulations in the case of stopped and inhomogeneous processes. One can obtain examples of additive functionals of a Markov process 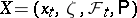 by setting
by setting 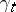 for
for 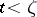 equal to
equal to 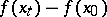 , or to
, or to 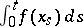 , or to the sum of the jumps of the random function
, or to the sum of the jumps of the random function 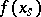 for
for 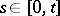 , where
, where 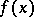 is bounded and measurable relative to
is bounded and measurable relative to 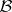 (the second and third examples are only valid under certain additional restrictions). Passing from any additive functional
(the second and third examples are only valid under certain additional restrictions). Passing from any additive functional 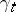 to
to 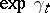 provides an example of a multiplicative functional. In the case of a standard Markov process, an interesting and important example of a multiplicative functional is given by the random function that is equal to 1 for
provides an example of a multiplicative functional. In the case of a standard Markov process, an interesting and important example of a multiplicative functional is given by the random function that is equal to 1 for 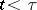 and to 0 for
and to 0 for 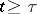 , where
, where  is the first exit moment of
is the first exit moment of 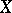 from some set
from some set 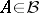 , that is,
, that is, 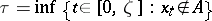 .
.
There is a natural transformation of a Markov process — passage to a subprocess — associated with multiplicative functionals, subject to the condition 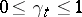 . From the transition function
. From the transition function 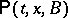 of the process
of the process 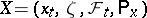 one constructs a new one,
one constructs a new one,
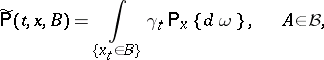 |
where it can happen that 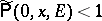 for certain points
for certain points 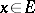 . The new transition function in
. The new transition function in 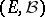 corresponds to some Markov process
corresponds to some Markov process 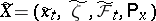 , which can be realized together with the original process on one and the same space of elementary events with the same measures
, which can be realized together with the original process on one and the same space of elementary events with the same measures 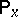 ,
, 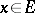 , and, moreover, such that
, and, moreover, such that 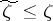 ,
, 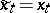 for
for 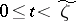 and such that the
and such that the 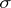 -algebra
-algebra  is the trace of
is the trace of 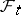 in the set
in the set 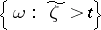 . The process
. The process 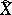 is called the subprocess of the Markov process
is called the subprocess of the Markov process 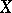 obtained as a result of "killing" or shortening the lifetime. The subprocess corresponding to the multiplicative functional in the previous example is called the part of
obtained as a result of "killing" or shortening the lifetime. The subprocess corresponding to the multiplicative functional in the previous example is called the part of 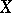 on the set
on the set 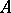 ; its phase space is naturally taken to be not the whole of
; its phase space is naturally taken to be not the whole of 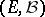 , but only
, but only 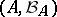 , where
, where 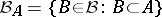 .
.
Additive functionals 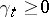 give rise to another type of transformation of Markov processes — a random time change — which reduces to changing the time of traversing the various sections of a trajectory. Suppose, for example, that
give rise to another type of transformation of Markov processes — a random time change — which reduces to changing the time of traversing the various sections of a trajectory. Suppose, for example, that 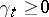 is a continuous additive functional of a standard Markov process
is a continuous additive functional of a standard Markov process 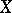 , with
, with 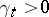 for
for 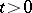 . Then
. Then 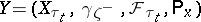 is a standard Markov process, where
is a standard Markov process, where 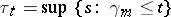 for
for 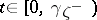 . Here one says that
. Here one says that 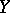 is obtained from
is obtained from 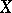 as a result of the random change
as a result of the random change 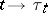 .
.
Various classes of additive functionals have been well studied, mainly of standard processes.
References
| [LS] | R.S. Liptser, A.N. Shiryaev, "Statistics of random processes" , 1–2 , Springer (1977–1978) (Translated from Russian) MR1800858 MR1800857 MR0608221 MR0488267 MR0474486 Zbl 1008.62073 Zbl 1008.62072 Zbl 0556.60003 Zbl 0369.60001 Zbl 0364.60004 |
| [D] | E.B. Dynkin, "Foundations of the theory of Markov processes" , Springer (1961) (Translated from Russian) MR0131898 |
| [D2] | E.B. Dynkin, "Markov processes" , 1–2 , Springer (1965) (Translated from Russian) MR0193671 Zbl 0132.37901 |
| [R] | D. Revuz, "Mesures associees aux fonctionelles additive de Markov I" Trans. Amer. Math. Soc. , 148 (1970) pp. 501–531 |
| [B] | A. Benveniste, "Application de deux théorèmes de G. Mokobodzki à l'étude du noyau de Lévy d'un processus de Hunt sans hypothèse (L)" , Lect. notes in math. , 321 , Springer (1973) pp. 1–24 MR0415781 MR0415782 |
Comments
The trace of an algebra of sets 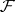 in
in  with respect to a subset
with respect to a subset 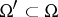 is the algebra of sets
is the algebra of sets 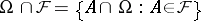 . It is a
. It is a 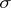 -algebra if
-algebra if 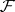 is a
is a 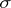 -algebra.
-algebra.
Functional of a Markov process. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Functional_of_a_Markov_process&oldid=26521