Difference between revisions of "Branching process with immigration"
From Encyclopedia of Mathematics
(→References: Seneta: right MR) |
(refs format) |
||
| Line 33: | Line 33: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017580/b01758024.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017580/b01758024.png" /></td> </tr></table> | ||
| − | it is necessary and sufficient | + | it is necessary and sufficient {{Cite|FW}} that |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017580/b01758025.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017580/b01758025.png" /></td> </tr></table> | ||
| − | This condition is met, in particular, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017580/b01758026.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017580/b01758027.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017580/b01758028.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017580/b01758029.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017580/b01758030.png" />, then | + | This condition is met, in particular, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017580/b01758026.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017580/b01758027.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017580/b01758028.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017580/b01758029.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017580/b01758030.png" />, then {{Cite|S}} |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017580/b01758031.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017580/b01758031.png" /></td> </tr></table> | ||
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017580/b01758032.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017580/b01758033.png" />, then there exists | + | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017580/b01758032.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017580/b01758033.png" />, then there exists {{Cite|S2}} a sequence of numbers <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017580/b01758034.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017580/b01758035.png" />, such that |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017580/b01758036.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b017/b017580/b01758036.png" /></td> </tr></table> | ||
| Line 54: | Line 54: | ||
====References==== | ====References==== | ||
| − | + | {| | |
| − | + | |valign="top"|{{Ref|Z}}|| A.M. Zubkov, "Life-like periods of a branching process with immigration" ''Theory Probab. Appl.'' , '''17''' : 1 (1972) pp. 174–183 ''Teor. Veroyatnost. i Primenen.'' , '''17''' : 1 (1972) pp. 179–188 {{MR|0300351}} {{ZBL|0267.60084}} | |
| − | + | |- | |
| − | + | |valign="top"|{{Ref|P}}|| A.G. Pakes, "Further results on the critical Galton–Watson process with immigration" ''J. Austral. Math. Soc.'' , '''13''' : 3 (1972) pp. 277–290 {{MR|0312585}} {{ZBL|0235.60078}} | |
| + | |- | ||
| + | |valign="top"|{{Ref|FW}}|| J.H. Foster, J.A. Williamson, "Limit theorems for the Galton–Watson process with time-dependent immigration" ''Z. Wahrsch. Verw. Geb.'' , '''20''' (1971) pp. 227–235 {{MR|0305494}} {{ZBL|0219.60069}} {{ZBL|0212.19702}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|S}}|| E. Seneta, "An explicit limit theorem for the critical Galton–Watson process with immigration" ''J. Roy. Statist. Soc. Ser. B'' , '''32''' : 1 (1970) pp. 149–152 {{MR|0266320}} {{ZBL|0198.52002}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|S2}}|| E. Seneta, "On the supercritical Galton–Watson process with immigration" ''Math. Biosci.'' , '''7''' (1970) pp. 9–14 {{MR|0270460}} {{ZBL|0209.48804}} | ||
| + | |- | ||
| + | |valign="top"|{{Ref|F}}|| J.H. Foster, "A limit theorem for a branching process with state-dependent immigration" ''Ann. of Math. Statist.'' , '''42''' : 5 (1971) pp. 1773–1776 {{MR|0348854}} {{ZBL|0245.60063}} | ||
| + | |} | ||
====Comments==== | ====Comments==== | ||
Additional references may be found in the article [[Branching process|Branching process]]. | Additional references may be found in the article [[Branching process|Branching process]]. | ||
Revision as of 06:19, 11 May 2012
2020 Mathematics Subject Classification: Primary: 60J80 [MSN][ZBL]
A model of a branching process (discrete-time or continuous-time, with one or several types of particles, etc.) in which new particles may appear not only as the products of division of the original particles, but also as a result of immigration from some "external source" . For instance, let
 |
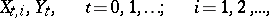be independent random variables with generating functions
 |
 |
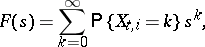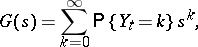respectively; the branching Galton–Watson process with immigration may be defined by the relations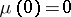 
, where 
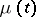is the number of particles and
 |
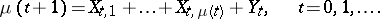Here, the variable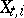 
is interpreted as the number of daughter particles of the 
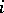-th particle of the 
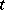-th generation, while the variable 
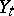is interpreted as the number of the particles which have immigrated into the 
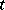-th generation. The generating functions
 |
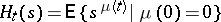are given by the recurrence relations
 |
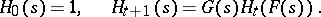The Markov chain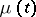 
corresponding to the Galton–Watson branching process with immigration is recurrent if 
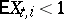and 
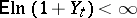or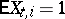 
and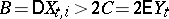 
, and is transient if 
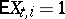and 
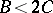or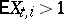 
. For the Markov chain 
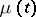to be ergodic, i.e. for the limits
 |
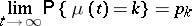to exist and to satisfy
 |
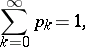it is necessary and sufficient [FW] that
 |
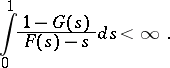This condition is met, in particular, if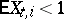 
and 
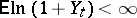. If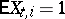 
, 
, 
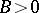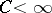, then [S]
 |
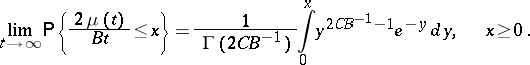If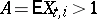 
and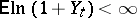 
, then there exists [S2] a sequence of numbers 
, 
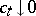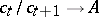, such that
 |
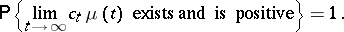In branching processes with immigration in which the immigration takes place at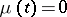 
only, i.e.
 |
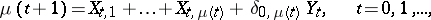where 
is the Kronecker symbol, the following relation is valid if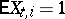 
, 
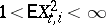and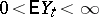 
:
 |
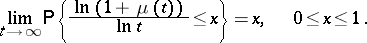References
| [Z] | A.M. Zubkov, "Life-like periods of a branching process with immigration" Theory Probab. Appl. , 17 : 1 (1972) pp. 174–183 Teor. Veroyatnost. i Primenen. , 17 : 1 (1972) pp. 179–188 MR0300351 Zbl 0267.60084 |
| [P] | A.G. Pakes, "Further results on the critical Galton–Watson process with immigration" J. Austral. Math. Soc. , 13 : 3 (1972) pp. 277–290 MR0312585 Zbl 0235.60078 |
| [FW] | J.H. Foster, J.A. Williamson, "Limit theorems for the Galton–Watson process with time-dependent immigration" Z. Wahrsch. Verw. Geb. , 20 (1971) pp. 227–235 MR0305494 Zbl 0219.60069 Zbl 0212.19702 |
| [S] | E. Seneta, "An explicit limit theorem for the critical Galton–Watson process with immigration" J. Roy. Statist. Soc. Ser. B , 32 : 1 (1970) pp. 149–152 MR0266320 Zbl 0198.52002 |
| [S2] | E. Seneta, "On the supercritical Galton–Watson process with immigration" Math. Biosci. , 7 (1970) pp. 9–14 MR0270460 Zbl 0209.48804 |
| [F] | J.H. Foster, "A limit theorem for a branching process with state-dependent immigration" Ann. of Math. Statist. , 42 : 5 (1971) pp. 1773–1776 MR0348854 Zbl 0245.60063 |
Comments
Additional references may be found in the article Branching process.
How to Cite This Entry:
Branching process with immigration. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Branching_process_with_immigration&oldid=26372
Branching process with immigration. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Branching_process_with_immigration&oldid=26372
This article was adapted from an original article by A.M. Zubkov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article