Difference between revisions of "Weierstrass coordinates"
From Encyclopedia of Mathematics
(Importing text file) |
m (began latex addition for simple elements in first paragraph) |
||
| Line 1: | Line 1: | ||
| − | A type of coordinates in an elliptic space. Let | + | A type of coordinates in an elliptic space. Let $M^n$ be an elliptic space obtained by the identification of diametrically-opposite points of the unit sphere $S^n$ in $(n+1)$-dimensional Euclidean space. The Weierstrass coordinates $(x_0 ,\ldots, x_n)$ of a point in $M^n$ are the orthogonal Cartesian coordinates of the point of $S^n$ that corresponds to it. Since the isometric mapping of $M^n$ into $S^n$ is not single-valued, Weierstrass coordinates are defined up to sign. A hyperplane in $M^n$ is given by a homogeneous linear equation |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097410/w09741010.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/w/w097/w097410/w09741010.png" /></td> </tr></table> | ||
Revision as of 10:06, 9 May 2012
A type of coordinates in an elliptic space. Let $M^n$ be an elliptic space obtained by the identification of diametrically-opposite points of the unit sphere $S^n$ in $(n+1)$-dimensional Euclidean space. The Weierstrass coordinates $(x_0 ,\ldots, x_n)$ of a point in $M^n$ are the orthogonal Cartesian coordinates of the point of $S^n$ that corresponds to it. Since the isometric mapping of $M^n$ into $S^n$ is not single-valued, Weierstrass coordinates are defined up to sign. A hyperplane in $M^n$ is given by a homogeneous linear equation
 |
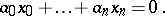Named after K. Weierstrass, who used these coordinates in his courses on Lobachevskii geometry in 1872.
Comments
These coordinates for elliptic space can be normalized so that
 |
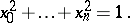The analogous Weierstrass coordinates for hyperbolic space satisfy
 |
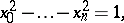with the same equation 
for a hyperplane.
References
| [a1] | H. Liebmann, "Nichteuklidische Geometrie" , Göschen (1912) pp. 114–119 |
| [a2] | H.S.M. Coxeter, "Non-Euclidean geometry" , Univ. Toronto Press (1965) pp. 121, 281 |
How to Cite This Entry:
Weierstrass coordinates. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weierstrass_coordinates&oldid=26263
Weierstrass coordinates. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Weierstrass_coordinates&oldid=26263
This article was adapted from an original article by E.V. Shikin (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article