Difference between revisions of "Node"
m |
m (→References) |
||
| Line 19: | Line 19: | ||
The node always has a polynomial Poincare-Dulac formal normal form, see [[Local normal forms for dynamical systems]], linear for non-resonant nodes and integrable in quadratures for resonant nodes. The transformation bringing an analytic node into its normal form always converges. | The node always has a polynomial Poincare-Dulac formal normal form, see [[Local normal forms for dynamical systems]], linear for non-resonant nodes and integrable in quadratures for resonant nodes. The transformation bringing an analytic node into its normal form always converges. | ||
| + | |||
| + | ====Differential and analytic type of nodes==== | ||
| + | Although all nodes sharing the same stability type are topologically equivalent, their $C^k$-smooth classification (for $k\ge 1$) is nontrivial. For simplicity, we will talk only about the "genuine" (planar) nodes of real analytic vector fields. The following types can be distinguished. | ||
| + | # ''Dicritical node'' with equal eigenvalues $(\lambda,\lambda)$ and ''diagonal'' linear part. The corresponding vector field has a continuum of [[separatrix|separatrices]] and can be analytically linearized to its topological normal form times a positive constant $|\lambda|>0$. | ||
| + | # ''Degenerate node'' with equal eigenvalues and nontrivial Jordan normal form of the linear part. This node has a single analytic separatrix but still can be analytically linearized. All other trajectories are [[characteristic trajectory|characteristic]] with the common limit direction. | ||
| + | # "Ordinary" ''resonant node'' with the ratio of eigenvalues $(\lambda:\mu)=(1:n)$, $n\in\N$, $n\ge 2$. This node also has only one analytic separatrix and is $C^{n-1}$-linearizable, but not $C^n$-linearizable in general. However, in the exceptional case the resonant node may have continuum of analytic separatrices and be analytically linearizable. | ||
| + | # "Ordinary" ''nonresonant node'' always has two analytic separatrices and is analytically linearizable. All trajectories except for two have the common limit direction which coincides with the eigenvector having the smallest (in the absolute value) eigenvalue. Two exceptional trajectories form the other separatrix tangent to the second eigenvector. | ||
| + | |||
| + | <center><img src="https://www.encyclopediaofmath.org/legacyimages/common_img/n066760g.gif" /><img src="https://www.encyclopediaofmath.org/legacyimages/common_img/n066760f.gif" /> | ||
| + | <img src="https://www.encyclopediaofmath.org/legacyimages/common_img/n066760e.gif" /></center> | ||
| + | |||
| + | |||
| + | |||
====References==== | ====References==== | ||
| Line 51: | Line 64: | ||
If the system (*) is linear (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066760/n06676041.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066760/n06676042.png" /> is a fixed matrix) then the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066760/n06676043.png" /> is a node only when the eigen values <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066760/n06676044.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066760/n06676045.png" /> are real and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066760/n06676046.png" />. Any ray <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066760/n06676047.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066760/n06676048.png" /> an eigen vector of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066760/n06676049.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066760/n06676050.png" /> a parameter) is a trajectory for it. Ordinary, degenerate and dicritical nodes for a linear system are depicted in Fig. d, Fig. eand Fig. f. | If the system (*) is linear (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066760/n06676041.png" />, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066760/n06676042.png" /> is a fixed matrix) then the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066760/n06676043.png" /> is a node only when the eigen values <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066760/n06676044.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066760/n06676045.png" /> are real and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066760/n06676046.png" />. Any ray <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066760/n06676047.png" /> (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066760/n06676048.png" /> an eigen vector of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066760/n06676049.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n066/n066760/n06676050.png" /> a parameter) is a trajectory for it. Ordinary, degenerate and dicritical nodes for a linear system are depicted in Fig. d, Fig. eand Fig. f. | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
Figure: n066760g | Figure: n066760g | ||
| Line 68: | Line 72: | ||
For references see [[Singular point|Singular point]] of a differential equation. | For references see [[Singular point|Singular point]] of a differential equation. | ||
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
Revision as of 06:22, 6 May 2012
The term which may refer to one of the following:
- A singular (non-smooth) point of an algebraic curve which is a transversal intersection of smooth branches;
- A vertex of the boundary of a nodal domain in the Harmonic analysis (related to the above and also to the [of the node in Physics]);
- A singular point of vector field of a special type (with all eigenvalues of the linear part being to one side of the imaginary axis);
- A point at which the function is evaluated for purposes of interpolation or numeric integration.
Node of a curve
For an algebraic (or analytic) planar curve, the node (or nodal point, also nodal singularity) is a point of self-intersection of smooth branches of the curve.
Example. For the curve $r =s\sin3\varphi$ (in the polar coordinates) the origin of coordinates is a node.

Warning. Often it is additionally required that the curve has only transversal self-intersections. In this case at most two smooth branches of the curve can cross each other at any given point, thus the above example will be not a node in this restricted sense.
Node of a vector field
A singular point of vector field $v(x)=Ax+\cdots$ (mostly on the plane, $x\in(\R^2,0)$, but higher-dimensional nodes in $(\R^n,0)$ are also considered) distinguished by the condition that the real part of all eigenvalues $\lambda_1,\dots,\lambda_n$ of the linear operator $A$ have the same sign. Thus the node can be stable, if $\operatorname{Re}\lambda_i<0$ for all $i=1,\dots,n$, and unstable if $\operatorname{Re}\lambda_i>0$ for all $i=1,\dots,n$. The stability is both in the Lyapunov sense and asymptotic (the unstable node is stable in the reverse time $\tau=-t$).
A stable (unstable) node is topologically equivalent to the standard node $\dot x=x$ (resp., $\dot x=-x$).
The node always has a polynomial Poincare-Dulac formal normal form, see Local normal forms for dynamical systems, linear for non-resonant nodes and integrable in quadratures for resonant nodes. The transformation bringing an analytic node into its normal form always converges.
Differential and analytic type of nodes
Although all nodes sharing the same stability type are topologically equivalent, their $C^k$-smooth classification (for $k\ge 1$) is nontrivial. For simplicity, we will talk only about the "genuine" (planar) nodes of real analytic vector fields. The following types can be distinguished.
- Dicritical node with equal eigenvalues $(\lambda,\lambda)$ and diagonal linear part. The corresponding vector field has a continuum of separatrices and can be analytically linearized to its topological normal form times a positive constant $|\lambda|>0$.
- Degenerate node with equal eigenvalues and nontrivial Jordan normal form of the linear part. This node has a single analytic separatrix but still can be analytically linearized. All other trajectories are characteristic with the common limit direction.
- "Ordinary" resonant node with the ratio of eigenvalues $(\lambda:\mu)=(1:n)$, $n\in\N$, $n\ge 2$. This node also has only one analytic separatrix and is $C^{n-1}$-linearizable, but not $C^n$-linearizable in general. However, in the exceptional case the resonant node may have continuum of analytic separatrices and be analytically linearizable.
- "Ordinary" nonresonant node always has two analytic separatrices and is analytically linearizable. All trajectories except for two have the common limit direction which coincides with the eigenvector having the smallest (in the absolute value) eigenvalue. Two exceptional trajectories form the other separatrix tangent to the second eigenvector.



References
| [a1] | J.L. Coolidge, "Algebraic plane curves" , Dover, reprint (1959) |
A node is a type of arrangement of the trajectories of an autonomous system of second-order ordinary differential equations
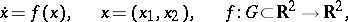 | (*) |
 ,
, 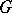 a domain of uniqueness, in a neighbourhood of a stationary point
a domain of uniqueness, in a neighbourhood of a stationary point 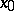 . This type is characterized in the following way. There exists a neighbourhood
. This type is characterized in the following way. There exists a neighbourhood  of
of  such that for all trajectories of the system beginning in
such that for all trajectories of the system beginning in  the negative semi-trajectories leave in the course of time any compact set
the negative semi-trajectories leave in the course of time any compact set 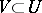 , while the positive semi-trajectories approach
, while the positive semi-trajectories approach 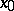 while not leaving
while not leaving 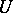 and, moreover, being completed with
and, moreover, being completed with 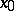 , touch it in well-defined directions, or vice versa. The point
, touch it in well-defined directions, or vice versa. The point 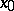 itself is also called a node, a nodal point or a basis point.
itself is also called a node, a nodal point or a basis point.
A node is either asymptotically stable in the sense of Lyapunov (cf. Lyapunov stability) or is totally unstable (asymptotically stable for 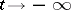 ). The Poincaré index of a node is 1 (cf. Singular point).
). The Poincaré index of a node is 1 (cf. Singular point).
For a system (*) of class 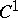 (
(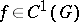 ) with non-zero matrix
) with non-zero matrix  , a stationary point
, a stationary point 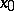 is a node if the eigen values
is a node if the eigen values 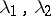 of
of 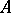 are real and satisfy the conditions
are real and satisfy the conditions 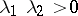 ,
, 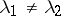 ; it can also be a node in cases when
; it can also be a node in cases when 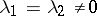 ,
, 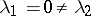 ,
, 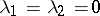 . In case
. In case 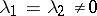 ,
,  will be a node if
will be a node if 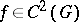 ; when this condition is not satisfied it may turn out to be focus. In any of the cases listed above the trajectories of the system converging to the node
; when this condition is not satisfied it may turn out to be focus. In any of the cases listed above the trajectories of the system converging to the node 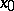 touch it in well-defined directions, defined by the eigen vectors of
touch it in well-defined directions, defined by the eigen vectors of 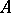 . If
. If 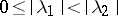 , there exist four such directions (if diametrically opposite ones are counted as distinct), and two trajectories of the system touch at
, there exist four such directions (if diametrically opposite ones are counted as distinct), and two trajectories of the system touch at 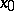 in directions corresponding to the eigen value
in directions corresponding to the eigen value  while two trajectories touch at
while two trajectories touch at 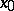 in directions corresponding to the eigen value
in directions corresponding to the eigen value 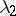 (Fig. a). These are ordinary nodes. If
(Fig. a). These are ordinary nodes. If 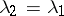 , then the eigen directions for
, then the eigen directions for 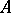 at
at 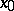 are either just two opposite directions (in this case the node is degenerate, cf. Fig. b) or all directions. In this last case, under the condition
are either just two opposite directions (in this case the node is degenerate, cf. Fig. b) or all directions. In this last case, under the condition 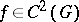 every direction is tangent at
every direction is tangent at 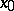 to a unique trajectory of the system. Such a node is called dicritical (Fig. c). VOL 5 COL 475 !
to a unique trajectory of the system. Such a node is called dicritical (Fig. c). VOL 5 COL 475 !
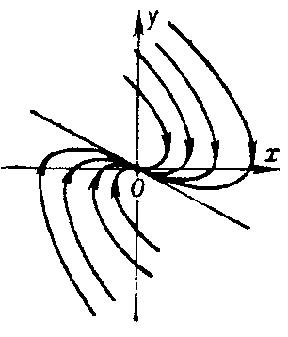
Figure: n066760b
VOL 5 COL 475 !
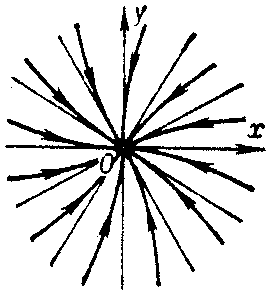
Figure: n066760c
VOL 5 COL 475 !
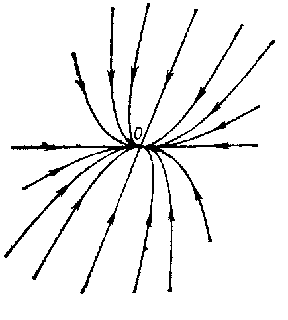
Figure: n066760d
If the system (*) is linear (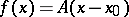 , where
, where 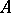 is a fixed matrix) then the point
is a fixed matrix) then the point 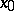 is a node only when the eigen values
is a node only when the eigen values 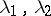 of
of 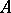 are real and
are real and  . Any ray
. Any ray 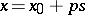 (
( an eigen vector of
an eigen vector of 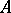 ,
, 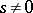 a parameter) is a trajectory for it. Ordinary, degenerate and dicritical nodes for a linear system are depicted in Fig. d, Fig. eand Fig. f.
a parameter) is a trajectory for it. Ordinary, degenerate and dicritical nodes for a linear system are depicted in Fig. d, Fig. eand Fig. f.
Figure: n066760g
In the case of an ordinary node all curvilinear trajectories are affine images of parabolas 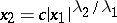 ,
, 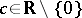 .
.
The term "node" is also applied to a stationary point of a system of the form (*) of order 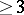 with analogous behaviour of the trajectories in neighbourhoods of it.
with analogous behaviour of the trajectories in neighbourhoods of it.
For references see Singular point of a differential equation.
Comments
References
| [a1] | S. Lefshetz, "Differential equations: geometric theory" , Dover, reprint (1977) pp. Sect. IX.2 |
| [a2] | G. Birkhoff, G.-C. Rota, "Ordinary differential equations" , Ginn (1962) pp. Sect. VI.8 |
Node. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Node&oldid=26083