Difference between revisions of "Continuous distribution"
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
(→References: Feller: internal link) |
||
| Line 16: | Line 16: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> W. Feller, "An introduction to probability theory and its applications" , '''2''' , Wiley (1971) | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> W. Feller, [[Feller, "An introduction to probability theory and its applications"|"An introduction to probability theory and its applications"]], '''2''', Wiley (1971) </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> M. Loève, "Probability theory", Princeton Univ. Press (1963) {{MR|0203748}} {{ZBL|0108.14202}} </TD></TR></table> |
| − | |||
| − | |||
====Comments==== | ====Comments==== | ||
Revision as of 09:26, 4 May 2012
2020 Mathematics Subject Classification: Primary: 60E05 [MSN][ZBL]
A probability distribution without atoms. Thus, a continuous distribution is the opposite of a discrete distribution (see also Atomic distribution). Discrete and continuous distributions together from the basic types of distributions. By a theorem of C. Jordan, every probability distribution is a mixture of a discrete and a continuous distribution. For example, let  be the distribution function corresponding to a certain distribution on the real line. Then
be the distribution function corresponding to a certain distribution on the real line. Then  , where
, where  and
and  are distribution functions of the discrete and the continuous type, respectively, is such a mixture. The distribution function of a continuous distribution is a continuous function. The absolutely-continuous distributions occupy a special position among the continuous distributions. This class of distributions
are distribution functions of the discrete and the continuous type, respectively, is such a mixture. The distribution function of a continuous distribution is a continuous function. The absolutely-continuous distributions occupy a special position among the continuous distributions. This class of distributions  on a measurable space
on a measurable space  is defined, relative to a reference measure
is defined, relative to a reference measure  , by the fact that
, by the fact that  can be represented in the form
can be represented in the form
 |
Here  is in
is in 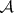 and
and 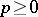 is a measurable function on
is a measurable function on  with
with 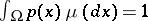 . The function
. The function 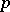 is called the density of
is called the density of  relative to
relative to  (usually,
(usually, 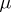 is Lebesgue measure and
is Lebesgue measure and  ). On the line, the corresponding distribution function
). On the line, the corresponding distribution function 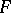 then has the representation
then has the representation
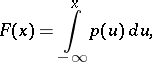 |
and here  almost-everywhere (with respect to Lebesgue measure). A distribution is absolutely continuous with respect to Lebesgue measure if and only if the corresponding distribution function is absolutely continuous (as a function of a real variable). In addition to absolutely-continuous distributions there are continuous distributions that are concentrated on sets of
almost-everywhere (with respect to Lebesgue measure). A distribution is absolutely continuous with respect to Lebesgue measure if and only if the corresponding distribution function is absolutely continuous (as a function of a real variable). In addition to absolutely-continuous distributions there are continuous distributions that are concentrated on sets of  -measure zero. Such distributions are called singular (cf. Singular distribution) with respect to a certain measure
-measure zero. Such distributions are called singular (cf. Singular distribution) with respect to a certain measure  . By Lebesgue's decomposition theorem, every continuous distribution is a mixture of two distributions, one of which is absolutely continuous and the other is singular with respect to
. By Lebesgue's decomposition theorem, every continuous distribution is a mixture of two distributions, one of which is absolutely continuous and the other is singular with respect to 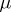 .
.
Some of the most important (absolutely-) continuous distributions are: the arcsine distribution; the beta-distribution, the gamma-distribution, the Cauchy distribution, the normal distribution, the uniform distribution, the exponential distribution, the Student distribution, and the "chi-squared" distribution.
References
| [1] | W. Feller, "An introduction to probability theory and its applications", 2, Wiley (1971) |
| [2] | M. Loève, "Probability theory", Princeton Univ. Press (1963) MR0203748 Zbl 0108.14202 |
Comments
Atoms are those points of the sample space that have positive probability. A discrete distribution is a distribution in which all probability is concentrated in the atoms.
An absolutely-continuous distribution 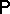 as defined above is also called absolutely continuous with respect to
as defined above is also called absolutely continuous with respect to 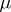 .
.
Continuous distribution. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Continuous_distribution&oldid=25948