Edgeworth series

2020 Mathematics Subject Classification: Primary: 60F05 [MSN][ZBL]

The series defined by

(*)

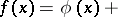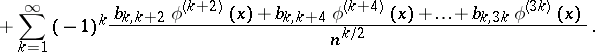Here is the distribution density of the random variable

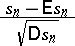(, where are independent and identically distributed),

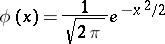is the density of the standard normal distribution, and

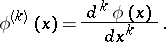The coefficients , , 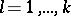do not depend on and are polynomials with respect to 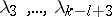, where , 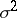is the variance, and 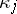is the semi-invariant of order 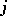of 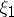. In particular, the first terms of the expansion have the form

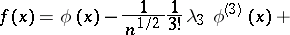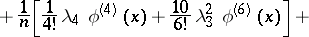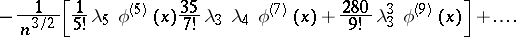The coefficients 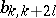can also be expressed in terms of the central moments.

The series (*) were introduced by F.Y. Edgeworth [1]. Their asymptotic properties have been studied by H. Cramér, who has shown that under fairly general conditions the series (*) is the asymptotic expansion of 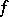in which the remainder has the order of the first discarded term.

References

[1]	F.Y. Edgeworth, "The law of error I" Proc. Cambridge Philos. Soc. , 20 (1905) pp. 36–65
[2]	H. Cramér, "Mathematical methods of statistics" , Princeton Univ. Press (1946) MR0016588 Zbl 0063.01014

Comments

The above discussion omits many technical details as well as modern developments.

An excellent account of the theory of Edgeworth expansions for sums of independent random variables is given in [a1]. See also [a2], Chapt. XVI for a brief and very smooth introduction to the theory of Edgeworth expansions. The case of sums of independent random vectors is treated in [a3]. Extensions to statistics of a more complicated structure, such as 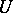-statistics — which are especially of interest in statistical theory — were studied by many authors over the last 15 years (as of 1988). An important recent contribution in this area is [a4].

References

[a1]	V.V. Petrov, "Sums of independent random variables", Springer (1975) (Translated from Russian) MR0388499 Zbl 0322.60043 Zbl 0322.60042
[a2]	W. Feller, "An introduction to probability theory and its applications", 2, Wiley (1971) pp. 135
[a3]	R.N. Bhattacharya, R. Ranga Rao, "Normal approximations and asymptotic expansions", Wiley (1976) MR0436272
[a4]	P.J. Bickel, F. Götze, W.R. van Zwet, "The Edgeworth expansion for 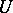-statistics of degree two" Ann. Statist., 14 (1986) pp. 1463–1484 MR868312