|
|
| Line 1: |
Line 1: |
| − | ''<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g0433102.png" />-function'' | + | ''$ $-function'' |
| | | | |
| − | A transcendental function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g0433103.png" /> that extends the values of the factorial <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g0433104.png" /> to any complex number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g0433105.png" />. It was introduced in 1729 by L. Euler in a letter to Ch. Goldbach, using the infinite product
| |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g0433106.png" /></td> </tr></table>
| + | A transcendental function $ $ that extends the values of the factorial $ $ to any complex number $ $. It was introduced in 1729 by L. Euler in a letter to Ch. Goldbach, using the infinite product |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g0433107.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| − | which was used by L. Euler to obtain the integral representation (Euler integral of the second kind, cf. [[Euler integrals|Euler integrals]])
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g0433108.png" /></td> </tr></table>
| + | which was used by L. Euler to obtain the integral representation (Euler integral of the second kind, cf. [[Euler integrals|Euler integrals]]) |
| | | | |
| − | which is valid for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g0433109.png" />. The multi-valuedness of the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331010.png" /> is eliminated by the formula <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331011.png" /> with a real <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331012.png" />. The symbol <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331013.png" /> and the name gamma-function were proposed in 1814 by A.M. Legendre.
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331014.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331015.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331016.png" /> the gamma-function may be represented by the Cauchy–Saalschütz integral:
| + | which is valid for $ $. The multi-valuedness of the function $ $ is eliminated by the formula $ $ with a real $ $. The symbol $ $ and the name gamma-function were proposed in 1814 by A.M. Legendre. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331017.png" /></td> </tr></table>
| + | If $ $ and $ $, $ $ the gamma-function may be represented by the Cauchy–Saalschütz integral: |
| | | | |
| − | In the entire plane punctured at the points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331018.png" /> the gamma-function satisfies a Hankel integral representation:
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331019.png" /></td> </tr></table>
| + | In the entire plane punctured at the points $ $ the gamma-function satisfies a Hankel integral representation: |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331020.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331021.png" /> is the branch of the logarithm for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331022.png" />; the contour <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331023.png" /> is represented in Fig. a. It is seen from the Hankel representation that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331024.png" /> is a [[Meromorphic function|meromorphic function]]. At the points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331025.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331026.png" /> it has simple poles with residues <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331027.png" />.
| + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | + | |
| | + | where $ $ and $ $ is the branch of the logarithm for which $ $; the contour $ $ is represented in Fig. a. It is seen from the Hankel representation that $ $ is a [[Meromorphic function|meromorphic function]]. At the points $ $, $ $ it has simple poles with residues $ $. |
| | | | |
| | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/g043310a.gif" /> | | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/g043310a.gif" /> |
| Line 28: |
Line 29: |
| | | | |
| | ==Fundamental relations and properties of the gamma-function.== | | ==Fundamental relations and properties of the gamma-function.== |
| − |
| |
| | | | |
| | 1) Euler's functional equation: | | 1) Euler's functional equation: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331028.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| | or | | or |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331029.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| − | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331030.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331031.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331032.png" /> is an integer; it is assumed that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331033.png" />.
| + | $ $, $ $ if $ $ is an integer; it is assumed that $ $. |
| | | | |
| | 2) Euler's completion formula: | | 2) Euler's completion formula: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331034.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| − | In particular, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331035.png" />; | + | In particular, $ $; |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331036.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| − | if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331037.png" /> is an integer; | + | if $ $ is an integer; |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331038.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| | 3) Gauss' multiplication formula: | | 3) Gauss' multiplication formula: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331039.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| − | If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331040.png" />, this is the Legendre duplication formula. | + | If $ $, this is the Legendre duplication formula. |
| | | | |
| − | 4) If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331041.png" /> or <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331042.png" />, then <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331043.png" /> can be asymptotically expanded into the Stirling series: | + | 4) If $ $ or $ $, then $ $ can be asymptotically expanded into the Stirling series: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331044.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331045.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331046.png" /> are the [[Bernoulli numbers|Bernoulli numbers]]. It implies the equality | + | where $ $ are the [[Bernoulli numbers|Bernoulli numbers]]. It implies the equality |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331047.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331048.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| | In particular, | | In particular, |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331049.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| | More accurate is Sonin's formula [[#References|[6]]]: | | More accurate is Sonin's formula [[#References|[6]]]: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331050.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| − | 5) In the real domain, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331051.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331052.png" /> and it assumes the sign <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331053.png" /> on the segments <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331054.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331055.png" /> (Fig. b). | + | 5) In the real domain, $ $ for $ $ and it assumes the sign $ $ on the segments $ $, $ $ (Fig. b). |
| | | | |
| | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/g043310b.gif" /> | | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/g043310b.gif" /> |
| Line 84: |
Line 84: |
| | Figure: g043310b | | Figure: g043310b |
| | | | |
| − | The graph of the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331056.png" />. | + | The graph of the function $ $. |
| | | | |
| − | For all real <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331057.png" /> the inequality | + | For all real $ $ the inequality |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331058.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| − | is valid, i.e. all branches of both <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331059.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331060.png" /> are convex functions. The property of logarithmic convexity defines the gamma-function among all solutions of the functional equation | + | is valid, i.e. all branches of both $ $ and $ $ are convex functions. The property of logarithmic convexity defines the gamma-function among all solutions of the functional equation |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331061.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| | up to a constant factor. | | up to a constant factor. |
| | | | |
| − | For positive values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331062.png" /> the gamma-function has a unique minimum at <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331063.png" /> equal to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331064.png" />. The local minima of the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331065.png" /> form a sequence tending to zero as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331066.png" />. | + | For positive values of $ $ the gamma-function has a unique minimum at $ $ equal to $ $. The local minima of the function $ $ form a sequence tending to zero as $ $. |
| | | | |
| | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/g043310c.gif" /> | | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/g043310c.gif" /> |
| Line 102: |
Line 102: |
| | Figure: g043310c | | Figure: g043310c |
| | | | |
| − | The graph of the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331067.png" />. | + | The graph of the function $ $. |
| | | | |
| − | 6) In the complex domain, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331068.png" />, the gamma-function rapidly decreases as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331069.png" />, | + | 6) In the complex domain, if $ $, the gamma-function rapidly decreases as $ $, |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331070.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| − | 7) The function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331071.png" /> (Fig. c) is an entire function of order one and of maximal type; asymptotically, as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331072.png" />, | + | 7) The function $ $ (Fig. c) is an entire function of order one and of maximal type; asymptotically, as $ $, |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331073.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| | where | | where |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331074.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| | It can be represented by the infinite Weierstrass product: | | It can be represented by the infinite Weierstrass product: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331075.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| − | which converges absolutely and uniformly on any compact set in the complex plane (<img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331076.png" /> is the [[Euler constant|Euler constant]]). A Hankel integral representation is valid: | + | which converges absolutely and uniformly on any compact set in the complex plane ($ $ is the [[Euler constant|Euler constant]]). A Hankel integral representation is valid: |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331077.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| − | where the contour <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331078.png" /> is shown in Fig. d. | + | where the contour $ $ is shown in Fig. d. |
| | | | |
| | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/g043310d.gif" /> | | <img style="border:1px solid;" src="https://www.encyclopediaofmath.org/legacyimages/common_img/g043310d.gif" /> |
| Line 130: |
Line 130: |
| | Figure: g043310d | | Figure: g043310d |
| | | | |
| − | <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331079.png" />
| + | $ $ |
| | | | |
| | G.F. Voronoi [[#References|[7]]] obtained integral representations for powers of the gamma-function. | | G.F. Voronoi [[#References|[7]]] obtained integral representations for powers of the gamma-function. |
| | | | |
| − | In applications, the so-called poly gamma-functions — <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331080.png" />-th derivatives of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331081.png" /> — are of importance. The function (Gauss' <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331083.png" />-function) | + | In applications, the so-called poly gamma-functions — $ $-th derivatives of $ $ — are of importance. The function (Gauss' $ $-function) |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331084.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331085.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| − | is meromorphic, has simple poles at the points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331086.png" /> and satisfies the functional equation | + | is meromorphic, has simple poles at the points $ $ and satisfies the functional equation |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331087.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| − | The representation of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331088.png" /> for <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331089.png" /> yields the formula | + | The representation of $ $ for $ $ yields the formula |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331090.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| | where | | where |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331091.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | + | |
| | + | This formula may be used to compute $ $ in a neighbourhood of the point $ $. |
| | + | |
| | + | For other poly gamma-functions see [[#References|[2]]]. The[[Incomplete gamma-function|incomplete gamma-function]] is defined by the equation |
| | + | |
| | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| − | This formula may be used to compute <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331092.png" /> in a neighbourhood of the point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331093.png" />.
| + | The functions $ $ and $ $ are transcendental functions which do not satisfy any linear differential equation with rational coefficients (Hölder's theorem). |
| | | | |
| − | For other poly gamma-functions see [[#References|[2]]]. The [[Incomplete gamma-function|incomplete gamma-function]] is defined by the equation
| + | The exceptional importance of the gamma-function in mathematical analysis is due to the fact that it can be used to express a large number of definite integrals, infinite products and sums of series (see, for example, [[Beta-function|Beta-function]]). In addition, it is widely used in the theory of special functions (the[[Hypergeometric function|hypergeometric function]], of which the gamma-function is a limit case, [[Cylinder functions|cylinder functions]], etc.), in analytic number theory, etc. |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331094.png" /></td> </tr></table>
| + | ====References==== |
| | | | |
| − | The functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331095.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331096.png" /> are transcendental functions which do not satisfy any linear differential equation with rational coefficients (Hölder's theorem).
| + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1952)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H. Bateman (ed.) A. Erdélyi (ed.) , ''Higher transcendental functions'' , '''1. The gamma function. The hypergeometric functions. Legendre functions''' , McGraw-Hill (1953)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. Functions of a real variable" , Addison-Wesley (1976) (Translated from French)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> , ''Math. anal., functions, limits, series, continued fractions'' , ''Handbook Math. Libraries'' , Moscow (1961) (In Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> N. Nielsen, "Handbuch der Theorie der Gammafunktion" , Chelsea, reprint (1965)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> N.Ya. Sonin, "Studies on cylinder functions and special polynomials" , Moscow (1954) (In Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> G.F. Voronoi, "Studies of primitive parallelotopes" , ''Collected works'' , '''2''' , Kiev (1952) pp. 239–368 (In Russian)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> E. Jahnke, F. Emde, "Tables of functions with formulae and curves" , Dover, reprint (1945) (Translated from German)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> A. Angot, "Compléments de mathématiques. A l'usage des ingénieurs de l'electrotechnique et des télécommunications" , C.N.E.T. (1957)</TD></TR></table> |
| | | | |
| − | The exceptional importance of the gamma-function in mathematical analysis is due to the fact that it can be used to express a large number of definite integrals, infinite products and sums of series (see, for example, [[Beta-function|Beta-function]]). In addition, it is widely used in the theory of special functions (the [[Hypergeometric function|hypergeometric function]], of which the gamma-function is a limit case, [[Cylinder functions|cylinder functions]], etc.), in analytic number theory, etc.
| |
| | | | |
| − | ====References====
| |
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1952)</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H. Bateman (ed.) A. Erdélyi (ed.) , ''Higher transcendental functions'' , '''1. The gamma function. The hypergeometric functions. Legendre functions''' , McGraw-Hill (1953)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> N. Bourbaki, "Elements of mathematics. Functions of a real variable" , Addison-Wesley (1976) (Translated from French)</TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> , ''Math. anal., functions, limits, series, continued fractions'' , ''Handbook Math. Libraries'' , Moscow (1961) (In Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> N. Nielsen, "Handbuch der Theorie der Gammafunktion" , Chelsea, reprint (1965)</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> N.Ya. Sonin, "Studies on cylinder functions and special polynomials" , Moscow (1954) (In Russian)</TD></TR><TR><TD valign="top">[7]</TD> <TD valign="top"> G.F. Voronoi, "Studies of primitive parallelotopes" , ''Collected works'' , '''2''' , Kiev (1952) pp. 239–368 (In Russian)</TD></TR><TR><TD valign="top">[8]</TD> <TD valign="top"> E. Jahnke, F. Emde, "Tables of functions with formulae and curves" , Dover, reprint (1945) (Translated from German)</TD></TR><TR><TD valign="top">[9]</TD> <TD valign="top"> A. Angot, "Compléments de mathématiques. A l'usage des ingénieurs de l'electrotechnique et des télécommunications" , C.N.E.T. (1957)</TD></TR></table>
| |
| | | | |
| | + | ====Comments==== |
| | | | |
| | + | The $ $-analogue of the gamma-function is given by |
| | | | |
| − | ====Comments==== | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| − | The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331098.png" />-analogue of the gamma-function is given by
| |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g04331099.png" /></td> </tr></table> | + | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;">$ $</td> </tr></table> |
| | | | |
| − | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g043310100.png" /></td> </tr></table>
| + | cf. [[#References|[a2]]]. Its origin goes back to E. Heine (1847) and D. Jackson (1904). For the gamma-function see also[[#References|[a1]]]. |
| | | | |
| − | cf. [[#References|[a2]]]. Its origin goes back to E. Heine (1847) and D. Jackson (1904). For the gamma-function see also [[#References|[a1]]].
| + | ====References==== |
| | | | |
| − | ====References====
| + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E. Artin, "The gamma function" , Holt, Rinehart & Winston (1964)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Askey, "The $ $-Gamma and $ $-Beta functions" ''Appl. Anal.'' , '''8''' (1978) pp. 125–141</TD></TR></table> |
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E. Artin, "The gamma function" , Holt, Rinehart & Winston (1964)</TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Askey, "The <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g043310101.png" />-Gamma and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043310/g043310102.png" />-Beta functions" ''Appl. Anal.'' , '''8''' (1978) pp. 125–141</TD></TR></table> | |
$ $-function
A transcendental function $ $ that extends the values of the factorial $ $ to any complex number $ $. It was introduced in 1729 by L. Euler in a letter to Ch. Goldbach, using the infinite product
which was used by L. Euler to obtain the integral representation (Euler integral of the second kind, cf. Euler integrals)
which is valid for $ $. The multi-valuedness of the function $ $ is eliminated by the formula $ $ with a real $ $. The symbol $ $ and the name gamma-function were proposed in 1814 by A.M. Legendre.
If $ $ and $ $, $ $ the gamma-function may be represented by the Cauchy–Saalschütz integral:
In the entire plane punctured at the points $ $ the gamma-function satisfies a Hankel integral representation:
where $ $ and $ $ is the branch of the logarithm for which $ $; the contour $ $ is represented in Fig. a. It is seen from the Hankel representation that $ $ is a meromorphic function. At the points $ $, $ $ it has simple poles with residues $ $.
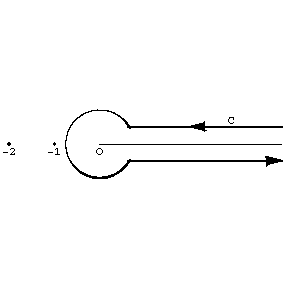
Figure: g043310a
Fundamental relations and properties of the gamma-function.
1) Euler's functional equation:
or
$ $, $ $ if $ $ is an integer; it is assumed that $ $.
2) Euler's completion formula:
In particular, $ $;
if $ $ is an integer;
3) Gauss' multiplication formula:
If $ $, this is the Legendre duplication formula.
4) If $ $ or $ $, then $ $ can be asymptotically expanded into the Stirling series:
where $ $ are the Bernoulli numbers. It implies the equality
In particular,
More accurate is Sonin's formula [6]:
5) In the real domain, $ $ for $ $ and it assumes the sign $ $ on the segments $ $, $ $ (Fig. b).
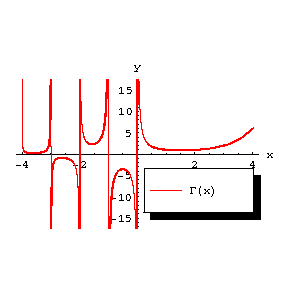
Figure: g043310b
The graph of the function $ $.
For all real $ $ the inequality
is valid, i.e. all branches of both $ $ and $ $ are convex functions. The property of logarithmic convexity defines the gamma-function among all solutions of the functional equation
up to a constant factor.
For positive values of $ $ the gamma-function has a unique minimum at $ $ equal to $ $. The local minima of the function $ $ form a sequence tending to zero as $ $.
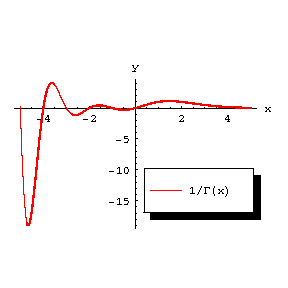
Figure: g043310c
The graph of the function $ $.
6) In the complex domain, if $ $, the gamma-function rapidly decreases as $ $,
7) The function $ $ (Fig. c) is an entire function of order one and of maximal type; asymptotically, as $ $,
where
It can be represented by the infinite Weierstrass product:
which converges absolutely and uniformly on any compact set in the complex plane ($ $ is the Euler constant). A Hankel integral representation is valid:
where the contour $ $ is shown in Fig. d.
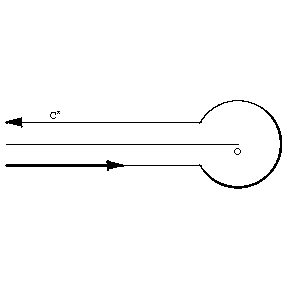
Figure: g043310d
$ $
G.F. Voronoi [7] obtained integral representations for powers of the gamma-function.
In applications, the so-called poly gamma-functions — $ $-th derivatives of $ $ — are of importance. The function (Gauss' $ $-function)
is meromorphic, has simple poles at the points $ $ and satisfies the functional equation
The representation of $ $ for $ $ yields the formula
where
This formula may be used to compute $ $ in a neighbourhood of the point $ $.
For other poly gamma-functions see [2]. Theincomplete gamma-function is defined by the equation
The functions $ $ and $ $ are transcendental functions which do not satisfy any linear differential equation with rational coefficients (Hölder's theorem).
The exceptional importance of the gamma-function in mathematical analysis is due to the fact that it can be used to express a large number of definite integrals, infinite products and sums of series (see, for example, Beta-function). In addition, it is widely used in the theory of special functions (thehypergeometric function, of which the gamma-function is a limit case, cylinder functions, etc.), in analytic number theory, etc.
References
| [1] | E.T. Whittaker, G.N. Watson, "A course of modern analysis" , Cambridge Univ. Press (1952) |
| [2] | H. Bateman (ed.) A. Erdélyi (ed.) , Higher transcendental functions , 1. The gamma function. The hypergeometric functions. Legendre functions , McGraw-Hill (1953) |
| [3] | N. Bourbaki, "Elements of mathematics. Functions of a real variable" , Addison-Wesley (1976) (Translated from French) |
| [4] | , Math. anal., functions, limits, series, continued fractions , Handbook Math. Libraries , Moscow (1961) (In Russian) |
| [5] | N. Nielsen, "Handbuch der Theorie der Gammafunktion" , Chelsea, reprint (1965) |
| [6] | N.Ya. Sonin, "Studies on cylinder functions and special polynomials" , Moscow (1954) (In Russian) |
| [7] | G.F. Voronoi, "Studies of primitive parallelotopes" , Collected works , 2 , Kiev (1952) pp. 239–368 (In Russian) |
| [8] | E. Jahnke, F. Emde, "Tables of functions with formulae and curves" , Dover, reprint (1945) (Translated from German) |
| [9] | A. Angot, "Compléments de mathématiques. A l'usage des ingénieurs de l'electrotechnique et des télécommunications" , C.N.E.T. (1957) |
The $ $-analogue of the gamma-function is given by
cf. [a2]. Its origin goes back to E. Heine (1847) and D. Jackson (1904). For the gamma-function see also[a1].
References
| [a1] | E. Artin, "The gamma function" , Holt, Rinehart & Winston (1964) |
| [a2] | R. Askey, "The $ $-Gamma and $ $-Beta functions" Appl. Anal. , 8 (1978) pp. 125–141 |



