Difference between revisions of "Steenrod problem"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 4: | Line 4: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> S. Eilenberg, "On the problems of topology" ''Ann. of Math.'' , '''50''' (1949) pp. 247–260 {{MR|0030189}} {{ZBL|0034.25304}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> R. Thom, "Quelques propriétés globales des variétés differentiables" ''Comm. Math. Helv.'' , '''28''' (1954) pp. 17–86 {{MR|0061823}} {{ZBL|0057.15502}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> P.E. Conner, E.E. Floyd, "Differentiable periodic maps" , Springer (1964) {{MR|0176478}} {{ZBL|0125.40103}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> R.E. Stong, "Notes on cobordism theory" , Princeton Univ. Press (1968) {{MR|0248858}} {{ZBL|0181.26604}} </TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> Yu.B. Rudyak, "Realization of homology classes of PL-manifolds with singularities" ''Math. Notes'' , '''41''' : 5 (1987) pp. 417–421 ''Mat. Zametki'' , '''41''' : 5 (1987) pp. 741–749 {{MR|898135}} {{ZBL|0632.57020}} </TD></TR></table> |
Revision as of 17:01, 15 April 2012
The problem of the realization of cycles (homology classes) by singular manifolds; formulated by N. Steenrod, cf. [1]. Let 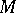 be a closed oriented manifold (topological, piecewise-linear, smooth, etc.) and let
be a closed oriented manifold (topological, piecewise-linear, smooth, etc.) and let 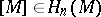 be its orientation (here
be its orientation (here 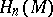 is the
is the  -dimensional homology group of
-dimensional homology group of 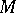 ). Any continuous mapping
). Any continuous mapping 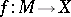 defines an element
defines an element 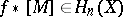 . The Steenrod problem consists of describing those homology classes of
. The Steenrod problem consists of describing those homology classes of 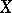 , called realizable, which are obtained in this way, i.e. which take the form
, called realizable, which are obtained in this way, i.e. which take the form 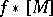 for a certain
for a certain 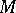 from the given class. All elements of the groups
from the given class. All elements of the groups 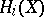 ,
, 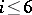 , are realizable by a smooth manifold. Any element of the group
, are realizable by a smooth manifold. Any element of the group 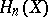 ,
, 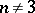 , is realizable by a mapping of a Poincaré complex
, is realizable by a mapping of a Poincaré complex 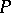 . Moreover, any cycle can be realized by a pseudo-manifold. Non-orientable manifolds can also be considered, and every homology class modulo
. Moreover, any cycle can be realized by a pseudo-manifold. Non-orientable manifolds can also be considered, and every homology class modulo  (i.e. element of
(i.e. element of 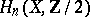 ) can be realized by a non-oriented smooth singular manifold
) can be realized by a non-oriented smooth singular manifold 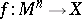 .
.
Thus, for smooth 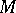 the Steenrod problem consists of describing the form of the homomorphism
the Steenrod problem consists of describing the form of the homomorphism 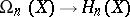 , where
, where 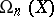 is the oriented bordism group of the space. The connection between the bordisms
is the oriented bordism group of the space. The connection between the bordisms 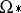 and the Thom spaces (cf. Thom space)
and the Thom spaces (cf. Thom space) 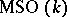 , discovered by R. Thom [2], clarified the Steenrod problem by reducing it to the study of the mappings
, discovered by R. Thom [2], clarified the Steenrod problem by reducing it to the study of the mappings 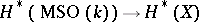 . A non-realizable class
. A non-realizable class 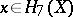 has been exhibited, where
has been exhibited, where  is the Eilenberg–MacLane space
is the Eilenberg–MacLane space 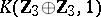 . For any class
. For any class  , some multiple
, some multiple 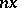 is realizable (by a smooth manifold); moreover,
is realizable (by a smooth manifold); moreover,  can be chosen odd.
can be chosen odd.
References
| [1] | S. Eilenberg, "On the problems of topology" Ann. of Math. , 50 (1949) pp. 247–260 MR0030189 Zbl 0034.25304 |
| [2] | R. Thom, "Quelques propriétés globales des variétés differentiables" Comm. Math. Helv. , 28 (1954) pp. 17–86 MR0061823 Zbl 0057.15502 |
| [3] | P.E. Conner, E.E. Floyd, "Differentiable periodic maps" , Springer (1964) MR0176478 Zbl 0125.40103 |
| [4] | R.E. Stong, "Notes on cobordism theory" , Princeton Univ. Press (1968) MR0248858 Zbl 0181.26604 |
| [5] | Yu.B. Rudyak, "Realization of homology classes of PL-manifolds with singularities" Math. Notes , 41 : 5 (1987) pp. 417–421 Mat. Zametki , 41 : 5 (1987) pp. 741–749 MR898135 Zbl 0632.57020 |
Steenrod problem. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Steenrod_problem&oldid=24570