Difference between revisions of "Regular ring (in commutative algebra)"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 8: | Line 8: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> O. Zariski, P. Samuel, "Commutative algebra" , '''2''' , Springer (1975) {{MR|0389876}} {{MR|0384768}} {{ZBL|0313.13001}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> J.-P. Serre, "Algèbre locale. Multiplicités" , ''Lect. notes in math.'' , '''11''' , Springer (1965) {{MR|0201468}} {{ZBL|0142.28603}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> A. Grothendieck, J. Dieudonné, "Eléments de géométrie algébrique. I. Le langage des schémas" ''Publ. Math. IHES'' , '''4''' (1964) {{MR|0173675}} {{ZBL|0118.36206}} </TD></TR></table> |
Revision as of 17:01, 15 April 2012
A Noetherian ring  whose localizations (cf. Localization in a commutative algebra)
whose localizations (cf. Localization in a commutative algebra)  are all regular (here
are all regular (here  is a prime ideal in
is a prime ideal in 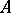 ). A local Noetherian ring
). A local Noetherian ring  (cf. Local ring) with maximal ideal
(cf. Local ring) with maximal ideal  is called regular if
is called regular if  is generated by
is generated by  elements, where
elements, where  , that is, if the tangent space
, that is, if the tangent space  (as a vector space over the field of residues) has dimension equal to
(as a vector space over the field of residues) has dimension equal to  . This is equivalent to the absence of singularities in the scheme
. This is equivalent to the absence of singularities in the scheme  . A regular local ring
. A regular local ring  is always integral and normal, and also factorial (cf. Factorial ring; the Auslander–Buchsbaum theorem), and its depth is equal to
is always integral and normal, and also factorial (cf. Factorial ring; the Auslander–Buchsbaum theorem), and its depth is equal to  (cf. Depth of a module). The associated graded ring
(cf. Depth of a module). The associated graded ring
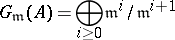 |
is isomorphic to the polynomial ring  . A local Noetherian ring
. A local Noetherian ring 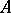 is regular if and only if its completion
is regular if and only if its completion  is regular; in general, if
is regular; in general, if  is a flat extension of local rings and
is a flat extension of local rings and 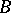 is regular, then
is regular, then 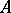 is also regular. For complete regular local rings, the Cohen structure theorem holds: Such a ring has the form
is also regular. For complete regular local rings, the Cohen structure theorem holds: Such a ring has the form  , where
, where  is a field or a discrete valuation ring. Any module of finite type over a regular local ring has a finite free resolution (see Hilbert theorem on syzygies); the converse also holds (see [2]).
is a field or a discrete valuation ring. Any module of finite type over a regular local ring has a finite free resolution (see Hilbert theorem on syzygies); the converse also holds (see [2]).
Fields and Dedekind rings are regular rings. If  is regular, then the ring of polynomials
is regular, then the ring of polynomials 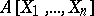 and the ring of formal power series
and the ring of formal power series  over
over 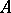 are also regular. If
are also regular. If  is a non-invertible element of a local regular ring, then
is a non-invertible element of a local regular ring, then  is regular if and only if
is regular if and only if  .
.
References
| [1] | O. Zariski, P. Samuel, "Commutative algebra" , 2 , Springer (1975) MR0389876 MR0384768 Zbl 0313.13001 |
| [2] | J.-P. Serre, "Algèbre locale. Multiplicités" , Lect. notes in math. , 11 , Springer (1965) MR0201468 Zbl 0142.28603 |
| [3] | A. Grothendieck, J. Dieudonné, "Eléments de géométrie algébrique. I. Le langage des schémas" Publ. Math. IHES , 4 (1964) MR0173675 Zbl 0118.36206 |
Regular ring (in commutative algebra). Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Regular_ring_(in_commutative_algebra)&oldid=24549