Difference between revisions of "Open book decomposition"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 6: | Line 6: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J.W. Alexander, "A lemma on systems of knotted curves" ''Proc. Nat. Acad. Sci. USA'' , '''9''' (1923) pp. 93–95 {{MR|}} {{ZBL|49.0408.03}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A.H. Durfee, H.B. Lawson Jr., "Fibered knots and foliations of highly connected manifolds" ''Invent. Math.'' , '''17''' (1972) pp. 203–215 {{MR|0326752}} {{ZBL|0231.57015}} </TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> T. Lawson, "Open book decompositions for odd dimensional manifolds" ''Topology'' , '''17''' (1978) pp. 189–192 {{MR|0494132}} {{ZBL|0384.57007}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> R. Myers, "Open book decompositions of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/o/o120/o120040/o12004015.png" />-manifolds" ''Proc. Amer. Math. Soc.'' , '''72''' (1978) pp. 397–402</TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> D. Rolfsen, "Knots and links" , Publish or Perish (1976) {{MR|0515288}} {{ZBL|0339.55004}} </TD></TR><TR><TD valign="top">[a6]</TD> <TD valign="top"> W.P. Thurston, H.E. Winkelnkemper, "On the existence of contact forms" ''Proc. Amer. Math. Soc.'' , '''52''' (1975) pp. 345–347 {{MR|0375366}} {{ZBL|0312.53028}} </TD></TR><TR><TD valign="top">[a7]</TD> <TD valign="top"> H.E. Winkelnkemper, "Manifolds as open books" ''Bull. Amer. Math. Soc.'' , '''79''' (1973) pp. 45–51 {{MR|0310912}} {{ZBL|0269.57011}} </TD></TR></table> |
Revision as of 17:00, 15 April 2012
Let 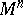 be an
be an  -dimensional manifold. An open book decomposition of
-dimensional manifold. An open book decomposition of 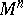 consists of a codimension-two submanifold
consists of a codimension-two submanifold 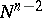 , called the binding, and a fibration
, called the binding, and a fibration 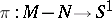 . The fibres are called the pages. One may require the fibration to be well behaved near
. The fibres are called the pages. One may require the fibration to be well behaved near 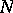 , i.e. that
, i.e. that 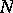 have a tubular neighbourhood
have a tubular neighbourhood 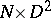 such that
such that 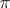 restricted to
restricted to 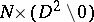 is the mapping
is the mapping 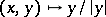 .
.
The existence of an open book decomposition for any closed, orientable  -manifold was proved by J.W. Alexander [a1]. He suggested that the binding may be assumed connected, but the first published proof of this fact was given by R. Myers [a4]. An independent proof (unpublished) is due to F.J. González-Acuña, see also [a5]. Any closed manifold of odd dimension
-manifold was proved by J.W. Alexander [a1]. He suggested that the binding may be assumed connected, but the first published proof of this fact was given by R. Myers [a4]. An independent proof (unpublished) is due to F.J. González-Acuña, see also [a5]. Any closed manifold of odd dimension  admits an open book decomposition [a3], and the same is true for any simply-connected manifold of even dimension
admits an open book decomposition [a3], and the same is true for any simply-connected manifold of even dimension 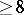 with vanishing index [a7].
with vanishing index [a7].
Such structure theorems have been used to give explicit geometric constructions of contact structures and codimension-one foliations; see, for instance, [a6], [a2].
References
| [a1] | J.W. Alexander, "A lemma on systems of knotted curves" Proc. Nat. Acad. Sci. USA , 9 (1923) pp. 93–95 Zbl 49.0408.03 |
| [a2] | A.H. Durfee, H.B. Lawson Jr., "Fibered knots and foliations of highly connected manifolds" Invent. Math. , 17 (1972) pp. 203–215 MR0326752 Zbl 0231.57015 |
| [a3] | T. Lawson, "Open book decompositions for odd dimensional manifolds" Topology , 17 (1978) pp. 189–192 MR0494132 Zbl 0384.57007 |
| [a4] | R. Myers, "Open book decompositions of  -manifolds" Proc. Amer. Math. Soc. , 72 (1978) pp. 397–402 -manifolds" Proc. Amer. Math. Soc. , 72 (1978) pp. 397–402 |
| [a5] | D. Rolfsen, "Knots and links" , Publish or Perish (1976) MR0515288 Zbl 0339.55004 |
| [a6] | W.P. Thurston, H.E. Winkelnkemper, "On the existence of contact forms" Proc. Amer. Math. Soc. , 52 (1975) pp. 345–347 MR0375366 Zbl 0312.53028 |
| [a7] | H.E. Winkelnkemper, "Manifolds as open books" Bull. Amer. Math. Soc. , 79 (1973) pp. 45–51 MR0310912 Zbl 0269.57011 |
Open book decomposition. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Open_book_decomposition&oldid=24521