Difference between revisions of "Cassini oval"
From Encyclopedia of Mathematics
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 15: | Line 15: | ||
Figure: c020700c | Figure: c020700c | ||
| − | A Cassini oval is the set of points (see Fig.) such that the product of the distances from each point to two given points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020700/c0207002.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020700/c0207003.png" /> (the foci) is constant. When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020700/c0207004.png" /> the Cassini oval is a convex curve; when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020700/c0207005.png" /> it is a curve with | + | A Cassini oval is the set of points (see Fig.) such that the product of the distances from each point to two given points <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020700/c0207002.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020700/c0207003.png" /> (the foci) is constant. When <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020700/c0207004.png" /> the Cassini oval is a convex curve; when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020700/c0207005.png" /> it is a curve with "waists" (concave parts); when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020700/c0207006.png" /> it is a [[Bernoulli lemniscate|Bernoulli lemniscate]]; and when <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/c/c020/c020700/c0207007.png" /> it consists of two components. Cassini ovals are related to [[Lemniscates|lemniscates]]. Cassini ovals were studied by G. Cassini (17th century) in his attempts to determine the Earth's orbit. |
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian)</TD></TR></table> |
| Line 26: | Line 26: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972) {{MR|1572089}} {{ZBL|0257.50002}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> J.W. Bruce, P.J. Giblin, "Curves and singularities: a geometrical introduction to singularity theory" , Cambridge Univ. Press (1984) {{MR|1541053}} {{ZBL|0534.58008}} </TD></TR></table> |
Revision as of 16:55, 15 April 2012
A plane algebraic curve of order four whose equation in Cartesian coordinates has the form:
 |
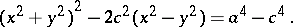Figure: c020700a
Figure: c020700b
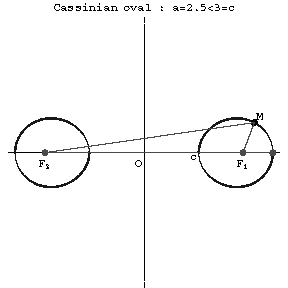
Figure: c020700c
A Cassini oval is the set of points (see Fig.) such that the product of the distances from each point to two given points 
and 
(the foci) is constant. When 
the Cassini oval is a convex curve; when 
it is a curve with "waists" (concave parts); when 
it is a Bernoulli lemniscate; and when 
it consists of two components. Cassini ovals are related to lemniscates. Cassini ovals were studied by G. Cassini (17th century) in his attempts to determine the Earth's orbit.
References
| [1] | A.A. Savelov, "Planar curves" , Moscow (1960) (In Russian) |
Comments
A Cassini oval is also called a Cassinian oval.
References
| [a1] | J.D. Lawrence, "A catalog of special plane curves" , Dover, reprint (1972) MR1572089 Zbl 0257.50002 |
| [a2] | J.W. Bruce, P.J. Giblin, "Curves and singularities: a geometrical introduction to singularity theory" , Cambridge Univ. Press (1984) MR1541053 Zbl 0534.58008 |
How to Cite This Entry:
Cassini oval. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cassini_oval&oldid=24392
Cassini oval. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Cassini_oval&oldid=24392
This article was adapted from an original article by D.D. Sokolov (originator), which appeared in Encyclopedia of Mathematics - ISBN 1402006098. See original article