Difference between revisions of "Boolean functions, metric theory of"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 1: | Line 1: | ||
| − | The branch of mathematics in which one studies numerical characteristics and metric properties of Boolean functions. The principal parts of this theory are concerned with properties of | + | The branch of mathematics in which one studies numerical characteristics and metric properties of Boolean functions. The principal parts of this theory are concerned with properties of "almost-all" Boolean functions (cf. [[Boolean functions, minimization of|Boolean functions, minimization of]]), properties of the set of all Boolean functions in a given number of variables, and special subclasses of Boolean functions. Another topic is the structure of the truth domains of Boolean functions with the aid of numerical characteristics that appear mainly in problems connected with the minimization of Boolean functions and the theory of local algorithms. These characteristics are the dimension and the extent of functions. |
Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b0169501.png" /> be the set of vertices of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b0169502.png" />-dimensional unit cube on which a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b0169503.png" /> is equal to one. Consider all maximal intervals of the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b0169504.png" /> and select the interval of the largest dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b0169505.png" />. The quantity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b0169506.png" /> is called the dimension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b0169507.png" /> and is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b0169508.png" />. In terms of the dimension one can estimate the complexity ratio of the most complex dead-end and the shortest disjunctive normal forms of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b0169509.png" /> (cf. [[Boolean functions, normal forms of|Boolean functions, normal forms of]]). An upper estimate of this ratio is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695010.png" />. The inequality | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b0169501.png" /> be the set of vertices of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b0169502.png" />-dimensional unit cube on which a function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b0169503.png" /> is equal to one. Consider all maximal intervals of the function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b0169504.png" /> and select the interval of the largest dimension <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b0169505.png" />. The quantity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b0169506.png" /> is called the dimension of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b0169507.png" /> and is denoted by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b0169508.png" />. In terms of the dimension one can estimate the complexity ratio of the most complex dead-end and the shortest disjunctive normal forms of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b0169509.png" /> (cf. [[Boolean functions, normal forms of|Boolean functions, normal forms of]]). An upper estimate of this ratio is <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695010.png" />. The inequality | ||
| Line 5: | Line 5: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695011.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695011.png" /></td> </tr></table> | ||
| − | is valid for | + | is valid for "almost-all" Boolean functions. |
| − | In solving problems of minimization of Boolean functions it is of interest to calculate the dimension of | + | In solving problems of minimization of Boolean functions it is of interest to calculate the dimension of "typical" maximal intervals. It has been proved that "almost-all" maximal intervals of "almost-all" Boolean functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695012.png" /> are of dimension close to <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695013.png" />. |
Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695014.png" /> be the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695015.png" />-th order smooth neighbourhood (cf. [[Algorithm, local|Algorithm, local]]) of an elementary conjunction <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695016.png" /> occurring in the abridged disjunctive normal form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695017.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695018.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695019.png" /> be the minimal value of the order of the neighbourhood in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695020.png" /> includes all elementary conjunctions occurring in the abridged disjunctive normal form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695021.png" />. The quantity | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695014.png" /> be the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695015.png" />-th order smooth neighbourhood (cf. [[Algorithm, local|Algorithm, local]]) of an elementary conjunction <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695016.png" /> occurring in the abridged disjunctive normal form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695017.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695018.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695019.png" /> be the minimal value of the order of the neighbourhood in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695020.png" /> includes all elementary conjunctions occurring in the abridged disjunctive normal form <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695021.png" />. The quantity | ||
| Line 13: | Line 13: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695022.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695022.png" /></td> </tr></table> | ||
| − | is called the extent of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695023.png" />. For | + | is called the extent of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695023.png" />. For "almost-all" Boolean functions |
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695024.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695024.png" /></td> </tr></table> | ||
| Line 25: | Line 25: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695040.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695040.png" /></td> </tr></table> | ||
| − | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695041.png" /> are constants. The construction of closed chains (cycles), i.e. of chains in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695042.png" />, with maximum cardinality of the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695043.png" /> is an important part of the proof of the theorem that the properties of conjunctions | + | where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695041.png" /> are constants. The construction of closed chains (cycles), i.e. of chains in which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695042.png" />, with maximum cardinality of the set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695043.png" /> is an important part of the proof of the theorem that the properties of conjunctions "of occurring in the minimal or shortest disjunctive normal form" are non-computable in the class of local algorithms. |
| − | The following result clarifies the structure of the truth domains of | + | The following result clarifies the structure of the truth domains of "almost-all" Boolean functions. A set <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695044.png" /> of vertices of the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695045.png" />-dimensional unit cube is called connected if for any point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695046.png" /> there exists a point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695047.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695048.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695049.png" />. A point <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695050.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695051.png" /> is called isolated if all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695052.png" /> such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695053.png" /> satisfy the condition <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695054.png" />. The following theorem holds: For "almost-all" Boolean functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695055.png" /> the set of ones, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695056.png" />, splits into the sum of a connected set and a set of isolated points. The cardinality of the connected set is not less than <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695057.png" /> and the number of isolated points does not exceed <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695058.png" />. |
| − | The results obtained in calculating the extent of | + | The results obtained in calculating the extent of "almost-all" Boolean functions are closely connected with the results obtained on calculating the radii and diameters of the graphs generated by Boolean functions. The graph <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695059.png" /> generated by a Boolean function <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695060.png" /> has as vertices the points of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695061.png" /> and as edges the pairs of points of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695062.png" /> at Hamming distance one from each other. The distance <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695063.png" /> between two vertices <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695064.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695065.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695066.png" /> is defined as the length of the shortest chain connecting <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695067.png" /> with <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695068.png" />. (It is assumed that the vertices <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695069.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695070.png" /> belong to the same connected component of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695071.png" />.) The deviation of the vertex <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695072.png" /> in <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695073.png" /> is the quantity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695074.png" />, where the maximum is taken over all the vertices of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695075.png" /> that belong to the same connected component as <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695076.png" />. The radius of a connected component <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695077.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695078.png" /> is the number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695079.png" />. The quantity <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695080.png" />, where the maximum is taken over all connected components of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695081.png" />, is called the radius of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695082.png" />. The diameter of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695083.png" /> is the number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695084.png" />, where the maximum is taken over all pairs of vertices <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695085.png" /> that belong to the same connected component. For "almost-all" Boolean functions <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695086.png" /> the quantities <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695087.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695088.png" /> are such that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695089.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695090.png" />. |
Of all the results of computations of numerical characteristics of individual classes of Boolean functions only those concerning monotone Boolean functions will be considered. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695091.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695092.png" /> be binary ordered samples. One says that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695093.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695094.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695095.png" />. A Boolean function is called monotone if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695096.png" /> implies that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695097.png" />. It is of interest to determine the exact number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695098.png" /> of distinct monotone Boolean functions in the variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695099.png" />. This number is known for only a few small values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b016950100.png" />. The asymptotic equality | Of all the results of computations of numerical characteristics of individual classes of Boolean functions only those concerning monotone Boolean functions will be considered. Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695091.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695092.png" /> be binary ordered samples. One says that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695093.png" /> if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695094.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695095.png" />. A Boolean function is called monotone if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695096.png" /> implies that <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695097.png" />. It is of interest to determine the exact number <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695098.png" /> of distinct monotone Boolean functions in the variables <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b01695099.png" />. This number is known for only a few small values of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/b/b016/b016950/b016950100.png" />. The asymptotic equality | ||
| Line 62: | Line 62: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> V.V. Glagolev, "Certain estimates of the disjunctive normal forms of functions of the algebra of logic" ''Problemy Kibernet.'' , '''19''' (1967) pp. 75–94 (In Russian) {{MR|225634}} {{ZBL|}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> Yu.I. Zhuravlev, "On algorithmic extraction of the set of essential variables of not everywhere defined functions of the algebra of logic" ''Problemy Kibernet.'' , '''11''' (1964) pp. 271–275 (In Russian)</TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> V.K. Korobkov, "On monotone functions of the algebra of logic" ''Problemy Kibernet.'' , '''13''' (1965) pp. 5–28 (In Russian) {{MR|209077}} {{ZBL|}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.A. Sapozhenko, "Metric properties of almost all functions of the algebras of logic" ''Diskret. Anal.'' , '''10''' (1967) pp. 91–119 (In Russian)</TD></TR><TR><TD valign="top">[5]</TD> <TD valign="top"> A.A. Sapozhenko, "The order of the neighbourhood of maximal intervals for almost all logical functions" ''Soviet Math. Dokl.'' , '''9''' : 3 (1968) pp. 591–594 ''Dokl. Akad. Nauk SSSR'' , '''180''' : 1 (1968) pp. 32–35</TD></TR><TR><TD valign="top">[6]</TD> <TD valign="top"> D.J. Kleitman, "On Dedekind's problem: the number of monotone Boolean functions" ''Proc. Amer. Math. Soc.'' , '''21''' (1969) pp. 677–682 {{MR|241334}} {{ZBL|}} </TD></TR></table> |
Revision as of 16:55, 15 April 2012
The branch of mathematics in which one studies numerical characteristics and metric properties of Boolean functions. The principal parts of this theory are concerned with properties of "almost-all" Boolean functions (cf. Boolean functions, minimization of), properties of the set of all Boolean functions in a given number of variables, and special subclasses of Boolean functions. Another topic is the structure of the truth domains of Boolean functions with the aid of numerical characteristics that appear mainly in problems connected with the minimization of Boolean functions and the theory of local algorithms. These characteristics are the dimension and the extent of functions.
Let 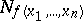 be the set of vertices of the
be the set of vertices of the  -dimensional unit cube on which a function
-dimensional unit cube on which a function  is equal to one. Consider all maximal intervals of the function
is equal to one. Consider all maximal intervals of the function 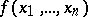 and select the interval of the largest dimension
and select the interval of the largest dimension  . The quantity
. The quantity  is called the dimension of
is called the dimension of 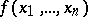 and is denoted by
and is denoted by  . In terms of the dimension one can estimate the complexity ratio of the most complex dead-end and the shortest disjunctive normal forms of
. In terms of the dimension one can estimate the complexity ratio of the most complex dead-end and the shortest disjunctive normal forms of 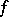 (cf. Boolean functions, normal forms of). An upper estimate of this ratio is
(cf. Boolean functions, normal forms of). An upper estimate of this ratio is 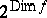 . The inequality
. The inequality
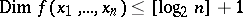 |
is valid for "almost-all" Boolean functions.
In solving problems of minimization of Boolean functions it is of interest to calculate the dimension of "typical" maximal intervals. It has been proved that "almost-all" maximal intervals of "almost-all" Boolean functions 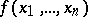 are of dimension close to
are of dimension close to 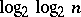 .
.
Let 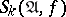 be the
be the 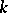 -th order smooth neighbourhood (cf. Algorithm, local) of an elementary conjunction
-th order smooth neighbourhood (cf. Algorithm, local) of an elementary conjunction 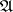 occurring in the abridged disjunctive normal form
occurring in the abridged disjunctive normal form 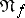 of
of 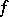 , and let
, and let  be the minimal value of the order of the neighbourhood in which
be the minimal value of the order of the neighbourhood in which 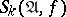 includes all elementary conjunctions occurring in the abridged disjunctive normal form
includes all elementary conjunctions occurring in the abridged disjunctive normal form 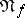 . The quantity
. The quantity
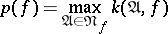 |
is called the extent of 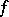 . For "almost-all" Boolean functions
. For "almost-all" Boolean functions
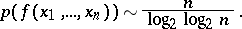 |
Let
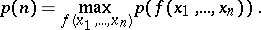 |
It is known that 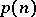 can be realized on a Boolean function of a special kind, which is called a chain. A function
can be realized on a Boolean function of a special kind, which is called a chain. A function 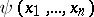 is called a chain if the set
is called a chain if the set 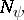 of its zeros can be represented as a sequence
of its zeros can be represented as a sequence 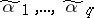 such that
such that 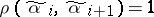 , where
, where 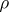 is the Hamming distance (cf. Code); the distance between other pairs
is the Hamming distance (cf. Code); the distance between other pairs 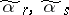 (possibly except for the pair (
(possibly except for the pair (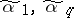 )) is larger than one, and no interval of dimension 2 is completely contained in the set of ones of
)) is larger than one, and no interval of dimension 2 is completely contained in the set of ones of 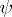 . The extent of the chain
. The extent of the chain 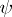 is
is 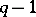 . Therefore, the problem of calculating
. Therefore, the problem of calculating 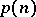 reduces to the construction of a chain with maximal
reduces to the construction of a chain with maximal 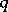 in the
in the  -dimensional unit cube. It has been shown by direct construction of such chains that
-dimensional unit cube. It has been shown by direct construction of such chains that
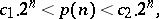 |
where 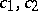 are constants. The construction of closed chains (cycles), i.e. of chains in which
are constants. The construction of closed chains (cycles), i.e. of chains in which 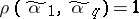 , with maximum cardinality of the set
, with maximum cardinality of the set 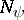 is an important part of the proof of the theorem that the properties of conjunctions "of occurring in the minimal or shortest disjunctive normal form" are non-computable in the class of local algorithms.
is an important part of the proof of the theorem that the properties of conjunctions "of occurring in the minimal or shortest disjunctive normal form" are non-computable in the class of local algorithms.
The following result clarifies the structure of the truth domains of "almost-all" Boolean functions. A set 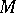 of vertices of the
of vertices of the  -dimensional unit cube is called connected if for any point
-dimensional unit cube is called connected if for any point 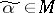 there exists a point
there exists a point 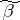 in
in 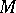 such that
such that 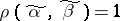 . A point
. A point 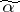 in
in 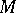 is called isolated if all
is called isolated if all 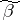 such that
such that 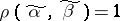 satisfy the condition
satisfy the condition 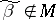 . The following theorem holds: For "almost-all" Boolean functions
. The following theorem holds: For "almost-all" Boolean functions 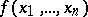 the set of ones,
the set of ones, 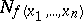 , splits into the sum of a connected set and a set of isolated points. The cardinality of the connected set is not less than
, splits into the sum of a connected set and a set of isolated points. The cardinality of the connected set is not less than 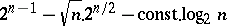 and the number of isolated points does not exceed
and the number of isolated points does not exceed  .
.
The results obtained in calculating the extent of "almost-all" Boolean functions are closely connected with the results obtained on calculating the radii and diameters of the graphs generated by Boolean functions. The graph 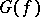 generated by a Boolean function
generated by a Boolean function  has as vertices the points of
has as vertices the points of 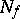 and as edges the pairs of points of
and as edges the pairs of points of 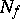 at Hamming distance one from each other. The distance
at Hamming distance one from each other. The distance 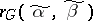 between two vertices
between two vertices 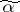 and
and 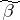 of
of 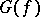 is defined as the length of the shortest chain connecting
is defined as the length of the shortest chain connecting 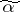 with
with 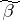 . (It is assumed that the vertices
. (It is assumed that the vertices 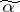 and
and 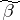 belong to the same connected component of
belong to the same connected component of 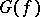 .) The deviation of the vertex
.) The deviation of the vertex 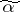 in
in 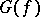 is the quantity
is the quantity 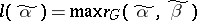 , where the maximum is taken over all the vertices of
, where the maximum is taken over all the vertices of 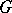 that belong to the same connected component as
that belong to the same connected component as 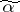 . The radius of a connected component
. The radius of a connected component 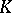 of
of 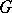 is the number
is the number 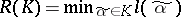 . The quantity
. The quantity 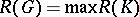 , where the maximum is taken over all connected components of
, where the maximum is taken over all connected components of 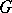 , is called the radius of
, is called the radius of 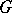 . The diameter of
. The diameter of 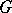 is the number
is the number 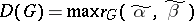 , where the maximum is taken over all pairs of vertices
, where the maximum is taken over all pairs of vertices 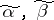 that belong to the same connected component. For "almost-all" Boolean functions
that belong to the same connected component. For "almost-all" Boolean functions 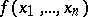 the quantities
the quantities 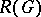 and
and 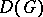 are such that
are such that 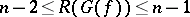 and
and 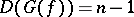 .
.
Of all the results of computations of numerical characteristics of individual classes of Boolean functions only those concerning monotone Boolean functions will be considered. Let  ,
, 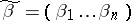 be binary ordered samples. One says that
be binary ordered samples. One says that 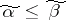 if
if 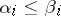 ,
, 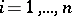 . A Boolean function is called monotone if
. A Boolean function is called monotone if 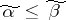 implies that
implies that 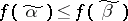 . It is of interest to determine the exact number
. It is of interest to determine the exact number 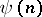 of distinct monotone Boolean functions in the variables
of distinct monotone Boolean functions in the variables  . This number is known for only a few small values of
. This number is known for only a few small values of  . The asymptotic equality
. The asymptotic equality
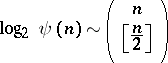 |
is also known.
The problem of optimal decoding of a monotone Boolean function has a large number of applications in the solution of discrete extremal problems. Consider a given algorithm 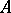 for the computation of a monotone Boolean function
for the computation of a monotone Boolean function  at any point
at any point 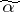 . If it can be established in the course of the computations that
. If it can be established in the course of the computations that  for some point
for some point 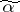 , then
, then 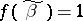 for all
for all 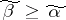 . If
. If 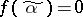 , the function
, the function 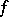 is known (and vanishes) at all points
is known (and vanishes) at all points 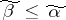 . Therefore, to effect the decoding, i.e. to completely reproduce the function
. Therefore, to effect the decoding, i.e. to completely reproduce the function  , the algorithm
, the algorithm 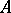 need only compute its values in a certain set of points. Let
need only compute its values in a certain set of points. Let 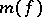 denote the minimum number of points sufficient to reproduce
denote the minimum number of points sufficient to reproduce 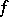 completely. Let
completely. Let
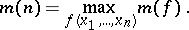 |
The quantity 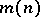 satisfies the asymptotic equality:
satisfies the asymptotic equality:
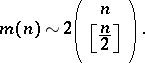 |
The estimate of 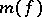 can be improved if supplementary information about the monotone Boolean function is available.
can be improved if supplementary information about the monotone Boolean function is available.
A problem related to the problem of decoding monotone Boolean functions is that of calculating numerical characteristics of the set of essential variables of Boolean functions that are not defined everywhere, i.e. functions defined on some subset of the set of vertices of the  -dimensional unit cube. A collection of variables
-dimensional unit cube. A collection of variables 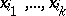 is called essential for a Boolean function
is called essential for a Boolean function 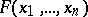 that is not everywhere defined if
that is not everywhere defined if  and if there exists a Boolean function
and if there exists a Boolean function 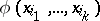 that is not everywhere defined such that
that is not everywhere defined such that  throughout the domain of definition of
throughout the domain of definition of 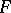 . An essential collection is called a dead-end collection for
. An essential collection is called a dead-end collection for 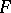 if no proper part of it is essential for
if no proper part of it is essential for 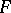 .
.
Each everywhere-defined Boolean function has a unique dead-end collection. For Boolean functions that are not defined everywhere the structure of the collections of essential variables is distinguished by its large variety. Let 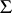 be the system of subsets of the set
be the system of subsets of the set 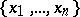 that satisfies the following condition: If
that satisfies the following condition: If 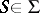 and if
and if 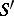 is an arbitrary subset of
is an arbitrary subset of  , then
, then 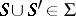 . Then there exists a Boolean function
. Then there exists a Boolean function 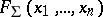 , not everywhere defined, such that
, not everywhere defined, such that 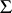 is a system of essential collections for
is a system of essential collections for  . Let
. Let 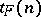 be the number of distinct dead-end collections for
be the number of distinct dead-end collections for 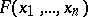 and put
and put
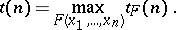 |
It is known that
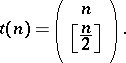 |
The algorithm for the construction of all dead-end collections for 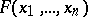 has maximal computational labour
has maximal computational labour 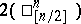 and this maximum is in fact attained. (Here the unit of labour is defined as the labour involved in verifying whether or not a given collection of variables is essential for
and this maximum is in fact attained. (Here the unit of labour is defined as the labour involved in verifying whether or not a given collection of variables is essential for 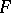 .)
.)
The metric theory of Boolean functions also deals with problems of computing characteristics connected with the problem of minimization of Boolean functions.
References
| [1] | V.V. Glagolev, "Certain estimates of the disjunctive normal forms of functions of the algebra of logic" Problemy Kibernet. , 19 (1967) pp. 75–94 (In Russian) MR225634 |
| [2] | Yu.I. Zhuravlev, "On algorithmic extraction of the set of essential variables of not everywhere defined functions of the algebra of logic" Problemy Kibernet. , 11 (1964) pp. 271–275 (In Russian) |
| [3] | V.K. Korobkov, "On monotone functions of the algebra of logic" Problemy Kibernet. , 13 (1965) pp. 5–28 (In Russian) MR209077 |
| [4] | A.A. Sapozhenko, "Metric properties of almost all functions of the algebras of logic" Diskret. Anal. , 10 (1967) pp. 91–119 (In Russian) |
| [5] | A.A. Sapozhenko, "The order of the neighbourhood of maximal intervals for almost all logical functions" Soviet Math. Dokl. , 9 : 3 (1968) pp. 591–594 Dokl. Akad. Nauk SSSR , 180 : 1 (1968) pp. 32–35 |
| [6] | D.J. Kleitman, "On Dedekind's problem: the number of monotone Boolean functions" Proc. Amer. Math. Soc. , 21 (1969) pp. 677–682 MR241334 |
Boolean functions, metric theory of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Boolean_functions,_metric_theory_of&oldid=24381