Difference between revisions of "Norm map"
(Importing text file) |
|||
| Line 17: | Line 17: | ||
<table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067350/n06735032.png" /></td> </tr></table> | <table class="eq" style="width:100%;"> <tr><td valign="top" style="width:94%;text-align:center;"><img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067350/n06735032.png" /></td> </tr></table> | ||
| − | where the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067350/n06735033.png" /> are all the isomorphisms of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067350/n06735034.png" /> into the [[Algebraic closure|algebraic closure]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067350/n06735035.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067350/n06735036.png" />. | + | where the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067350/n06735033.png" /> are all the isomorphisms of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067350/n06735034.png" /> into the [[Algebraic closure|algebraic closure]] <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067350/n06735035.png" /> of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067350/n06735036.png" /> fixing the elements of $k$. |
The norm map is transitive. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067350/n06735037.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067350/n06735038.png" /> are finite extensions, then | The norm map is transitive. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067350/n06735037.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/n/n067/n067350/n06735038.png" /> are finite extensions, then | ||
Revision as of 21:45, 14 April 2012
The mapping 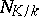 of a field
of a field 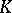 into a field
into a field 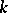 , where
, where  is a finite extension of
is a finite extension of 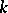 (cf. Extension of a field), that sends an element
(cf. Extension of a field), that sends an element 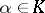 to the element
to the element  that is the determinant of the matrix of the
that is the determinant of the matrix of the 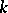 -linear mapping
-linear mapping 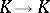 that takes
that takes 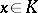 to
to 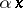 . The element
. The element 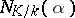 is called the norm of the element
is called the norm of the element 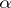 .
.
One has 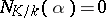 if and only if
if and only if 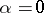 . For any
. For any 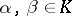 ,
,
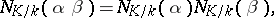 |
that is, 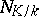 induces a homomorphism of the multiplicative groups
induces a homomorphism of the multiplicative groups 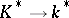 , which is also called the norm map. For any
, which is also called the norm map. For any 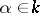 ,
,
 |
The group  is called the norm subgroup of
is called the norm subgroup of  , or the group of norms (from
, or the group of norms (from 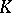 into
into 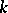 ). If
). If  is the characteristic polynomial of
is the characteristic polynomial of 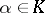 relative to
relative to 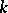 , then
, then
 |
Suppose that 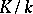 is separable (cf. Separable extension). Then for any
is separable (cf. Separable extension). Then for any 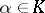 ,
,
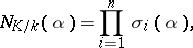 |
where the 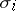 are all the isomorphisms of
are all the isomorphisms of 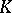 into the algebraic closure
into the algebraic closure  of
of 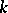 fixing the elements of $k$.
fixing the elements of $k$.
The norm map is transitive. If  and
and 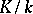 are finite extensions, then
are finite extensions, then
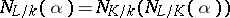 |
for any 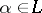 .
.
References
| [1] | S. Lang, "Algebra" , Addison-Wesley (1984) |
| [2] | Z.I. Borevich, I.R. Shafarevich, "Number theory" , Acad. Press (1966) (Translated from Russian) (German translation: Birkhäuser, 1966) |
Norm map. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Norm_map&oldid=24335