Difference between revisions of "Modules, category of"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 16: | Line 16: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Bass, "Algebraic <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/m/m064/m064480/m06448036.png" />-theory" , Benjamin (1968) {{MR|249491}} {{ZBL|}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> I. Bucur, A. Deleanu, "Introduction to the theory of categories and functors" , Wiley (1968) {{MR|0236236}} {{ZBL|0197.29205}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> C. Faith, "Algebra: rings, modules and categories" , '''1–2''' , Springer (1973–1976) {{MR|0551052}} {{MR|0491784}} {{MR|0366960}} {{ZBL|0508.16001}} {{ZBL|0266.16001}} </TD></TR></table> |
Revision as of 17:34, 31 March 2012
The category mod- whose objects are the right unitary modules over an arbitrary associative ring
whose objects are the right unitary modules over an arbitrary associative ring  with identity, and whose morphisms are the homomorphisms of
with identity, and whose morphisms are the homomorphisms of  -modules. This category is the most important example of an Abelian category. Moreover, for every small Abelian category there is a full exact imbedding into some category of modules.
-modules. This category is the most important example of an Abelian category. Moreover, for every small Abelian category there is a full exact imbedding into some category of modules.
If  , the ring of integers, then mod-
, the ring of integers, then mod-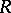 is the category of Abelian groups, and if
is the category of Abelian groups, and if  is a skew-field, then mod-
is a skew-field, then mod- is the category of vector spaces over
is the category of vector spaces over  .
.
The properties of mod- reflect a number of important properties of the ring
reflect a number of important properties of the ring 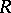 (see Homological classification of rings). Connected with this category is a number of important homological invariants of the ring; in particular, its homological dimension. The centre of mod-
(see Homological classification of rings). Connected with this category is a number of important homological invariants of the ring; in particular, its homological dimension. The centre of mod-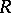 (that is, the set of natural transformations of the identity functor of the category) is isomorphic to the centre of
(that is, the set of natural transformations of the identity functor of the category) is isomorphic to the centre of  .
.
In ring theory, homological algebra and algebraic 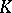 -theory, various subcategories of the category of modules are discussed; in particular, the subcategory of finitely-generated projective
-theory, various subcategories of the category of modules are discussed; in particular, the subcategory of finitely-generated projective 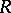 -modules and the associated
-modules and the associated  -functors (see Algebraic
-functors (see Algebraic  -theory). By analogy with Pontryagin duality, dualities between full subcategories of the category of modules have been studied; in particular between subcategories of finitely-generated modules. For example, it has been established that if
-theory). By analogy with Pontryagin duality, dualities between full subcategories of the category of modules have been studied; in particular between subcategories of finitely-generated modules. For example, it has been established that if  and
and 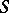 are Noetherian rings and if there is duality between finitely-generated right
are Noetherian rings and if there is duality between finitely-generated right  -modules and finitely-generated left
-modules and finitely-generated left  -modules, then there is a bimodule
-modules, then there is a bimodule  such that the given duality is equivalent to the duality defined by the functors
such that the given duality is equivalent to the duality defined by the functors
 |
the ring of endomorphisms 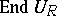 is isomorphic to
is isomorphic to 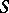 ,
,  is isomorphic to
is isomorphic to  , the bimodule
, the bimodule  is a finitely-generated injective cogenerator (both as an
is a finitely-generated injective cogenerator (both as an  -module and an
-module and an 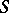 -module), and the ring
-module), and the ring 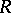 is semi-perfect (cf. Semi-perfect ring). The most important class of rings, arising in the consideration of duality of modules, is the class of quasi-Frobenius rings (cf. Quasi-Frobenius ring). A left Artinian ring
is semi-perfect (cf. Semi-perfect ring). The most important class of rings, arising in the consideration of duality of modules, is the class of quasi-Frobenius rings (cf. Quasi-Frobenius ring). A left Artinian ring  is quasi-Frobenius if and only if the mapping
is quasi-Frobenius if and only if the mapping
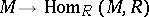 |
defines a duality between the categories of finitely-generated left and right 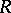 -modules.
-modules.
References
| [1] | H. Bass, "Algebraic 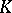 -theory" , Benjamin (1968) MR249491 -theory" , Benjamin (1968) MR249491 |
| [2] | I. Bucur, A. Deleanu, "Introduction to the theory of categories and functors" , Wiley (1968) MR0236236 Zbl 0197.29205 |
| [3] | C. Faith, "Algebra: rings, modules and categories" , 1–2 , Springer (1973–1976) MR0551052 MR0491784 MR0366960 Zbl 0508.16001 Zbl 0266.16001 |
Comments
A duality given by a bimodule  as described above is called a
as described above is called a  -duality or Morita duality; cf. also (the comments to) Morita equivalence.
-duality or Morita duality; cf. also (the comments to) Morita equivalence.
Modules, category of. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Modules,_category_of&oldid=24108