Difference between revisions of "Lagrange method"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 28: | Line 28: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , '''1''' , Chelsea, reprint (1977) (Translated from Russian) {{MR|1657129}} {{MR|0107649}} {{MR|0107648}} {{ZBL|0927.15002}} {{ZBL|0927.15001}} {{ZBL|0085.01001}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> A.G. Kurosh, "Higher algebra" , MIR (1972) (Translated from Russian) {{MR|0945393}} {{MR|0926059}} {{MR|0778202}} {{MR|0759341}} {{MR|0628003}} {{MR|0384363}} {{ZBL|0237.13001}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> P.S. Aleksandrov, "Lectures on analytical geometry" , Moscow (1968) (In Russian) {{MR|0244836}} {{ZBL|}} </TD></TR></table> |
Revision as of 17:33, 31 March 2012
A method for reducing a quadratic form (cf. also Quadratic forms, reduction of) to a sum of squares, given by J.L. Lagrange in 1759. Suppose one is given a quadratic form
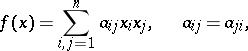 | (1) |
in  variables
variables  , with coefficients from a field
, with coefficients from a field 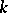 of characteristic
of characteristic 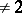 . It is required to reduce this form to the canonical form
. It is required to reduce this form to the canonical form
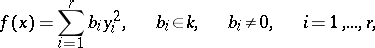 | (2) |
by means of a non-singular linear transformation of the variables. Lagrange's method consists in the following. One may assume that not all the coefficients in (1) are zero. Therefore, two cases are possible.
1) For some 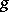 ,
, 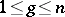 , the diagonal coefficient
, the diagonal coefficient 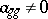 . Then
. Then
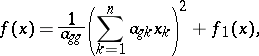 | (3) |
where the form 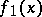 does not contain the variable
does not contain the variable 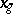 .
.
2) If all the  , but
, but  , then
, then
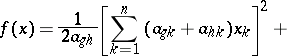 | (4) |
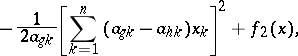 |
where the form 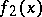 does not contain the two variables
does not contain the two variables 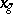 and
and 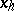 . The forms in square brackets in (4) are linearly independent. By using transformations of the form (3) and (4), after finitely many steps one can reduce the form (1) to a sum of squares of linearly independent linear forms. By means of partial derivatives the formulas (3) and (4) can be written as
. The forms in square brackets in (4) are linearly independent. By using transformations of the form (3) and (4), after finitely many steps one can reduce the form (1) to a sum of squares of linearly independent linear forms. By means of partial derivatives the formulas (3) and (4) can be written as
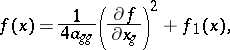 |
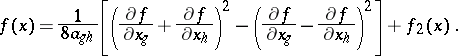 |
References
| [1] | F.R. [F.R. Gantmakher] Gantmacher, "The theory of matrices" , 1 , Chelsea, reprint (1977) (Translated from Russian) MR1657129 MR0107649 MR0107648 Zbl 0927.15002 Zbl 0927.15001 Zbl 0085.01001 |
| [2] | A.G. Kurosh, "Higher algebra" , MIR (1972) (Translated from Russian) MR0945393 MR0926059 MR0778202 MR0759341 MR0628003 MR0384363 Zbl 0237.13001 |
| [3] | P.S. Aleksandrov, "Lectures on analytical geometry" , Moscow (1968) (In Russian) MR0244836 |
Comments
See also Law of inertia.
Lagrange method. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Lagrange_method&oldid=24094