Difference between revisions of "Galois theory of rings"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 13: | Line 13: | ||
2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318020.png" />; | 2) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318020.png" />; | ||
| − | 3) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318021.png" />. Unlike the Galois theory of fields, (even when the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318022.png" /> is finite) the equality <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318023.png" /> is not always valid, while the correspondences 1), 2) and 1), 3) need not be mutually inverse. It is of interest, accordingly, to single out families of subrings and families of subgroups for which the analogue of the theorem on [[Galois correspondence|Galois correspondence]] is valid. This problem has found a positive solution in two cases. The first one involves the requirements of | + | 3) <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318021.png" />. Unlike the Galois theory of fields, (even when the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318022.png" /> is finite) the equality <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318023.png" /> is not always valid, while the correspondences 1), 2) and 1), 3) need not be mutually inverse. It is of interest, accordingly, to single out families of subrings and families of subgroups for which the analogue of the theorem on [[Galois correspondence|Galois correspondence]] is valid. This problem has found a positive solution in two cases. The first one involves the requirements of "proximity" between the properties of the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318024.png" /> and the properties of a field (e.g. <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318025.png" /> is a skew-field or a complete ring of linear transformations of a vector space over a skew-field); the second is the requirement of "proximity" between the structure of the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318026.png" /> over a subring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318027.png" /> to the structure of the corresponding pair if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318028.png" /> is a field (e.g. the <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318029.png" />-module is projective). |
Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318030.png" /> be an invertible element of the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318031.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318032.png" /> be the automorphism of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318033.png" /> defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318034.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318035.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318036.png" /> be the subalgebra of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318037.png" /> generated by the invertible elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318038.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318039.png" />. The group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318040.png" /> is called an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318042.png" />-group if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318043.png" /> for all invertible <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318044.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318045.png" /> is a skew-field, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318046.png" /> is a sub-skew-field of it, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318047.png" />, and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318048.png" /> is a finite-dimensional left vector space over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318049.png" />, then the Galois correspondences <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318050.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318051.png" /> are mutually inverse, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318052.png" /> belongs to the set of all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318053.png" />-subgroups of the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318054.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318055.png" /> to the set of all skew-fields of the sub-skew-field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318056.png" /> containing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318057.png" />. | Let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318030.png" /> be an invertible element of the ring <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318031.png" />, let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318032.png" /> be the automorphism of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318033.png" /> defined by <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318034.png" />, <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318035.png" />, and let <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318036.png" /> be the subalgebra of <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318037.png" /> generated by the invertible elements <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318038.png" /> for which <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318039.png" />. The group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318040.png" /> is called an <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318042.png" />-group if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318043.png" /> for all invertible <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318044.png" />. If <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318045.png" /> is a skew-field, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318046.png" /> is a sub-skew-field of it, if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318047.png" />, and if <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318048.png" /> is a finite-dimensional left vector space over <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318049.png" />, then the Galois correspondences <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318050.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318051.png" /> are mutually inverse, where <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318052.png" /> belongs to the set of all <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318053.png" />-subgroups of the group <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318054.png" /> and <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318055.png" /> to the set of all skew-fields of the sub-skew-field <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318056.png" /> containing <img align="absmiddle" border="0" src="https://www.encyclopediaofmath.org/legacyimages/g/g043/g043180/g04318057.png" />. | ||
| Line 30: | Line 30: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956) {{MR|0081264}} {{ZBL|0073.02002}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> S.U. Chase, M.E. Swedler, "Hopf algebras and Galois theory" , Springer (1969) {{MR|0260724}} {{ZBL|0197.01403}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> F. de Meyer, E. Ingraham, "Separable algebras over commutative rings" , ''Lect. notes in math.'' , '''181''' , Springer (1971) {{MR|280479}} {{ZBL|}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> A.R. Magid, "The separable Galois theory of commutative rings" , M. Dekker (1974) {{MR|0352075}} {{ZBL|0284.13004}} </TD></TR></table> |
| Line 38: | Line 38: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> S.U. Chase, D.K. Harrison, A. Rosenberg, "Galois theory and Galois cohomology of commutative rings" , ''Mem. Amer. Math. Soc.'' , '''52''' , Amer. Math. Soc. (1965) {{MR|0195922}} {{ZBL|0143.05902}} </TD></TR></table> |
Revision as of 17:32, 31 March 2012
A generalization of the results of the theory of Galois fields (cf. Galois theory and Galois group) to the case of associative rings with a unit element. Let  be an associative ring with a unit element, let
be an associative ring with a unit element, let 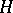 be some subgroup of the group of all automorphisms of
be some subgroup of the group of all automorphisms of  , let
, let 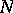 be a subgroup of
be a subgroup of 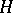 , let
, let
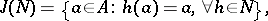 |
and let  . The set
. The set 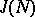 will then be a subring of
will then be a subring of  . Let
. Let  be a subring of
be a subring of 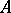 . One says that an automorphism
. One says that an automorphism 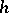 of
of 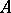 leaves
leaves 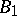 invariant elementwise if
invariant elementwise if 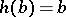 for all
for all 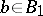 . The set of all such automorphisms is denoted by
. The set of all such automorphisms is denoted by 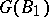 . Let
. Let
 |
The principal subject of the Galois theory of rings are the correspondences:
1) 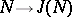 ;
;
2) 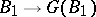 ;
;
3) 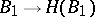 . Unlike the Galois theory of fields, (even when the group
. Unlike the Galois theory of fields, (even when the group 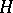 is finite) the equality
is finite) the equality 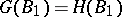 is not always valid, while the correspondences 1), 2) and 1), 3) need not be mutually inverse. It is of interest, accordingly, to single out families of subrings and families of subgroups for which the analogue of the theorem on Galois correspondence is valid. This problem has found a positive solution in two cases. The first one involves the requirements of "proximity" between the properties of the ring
is not always valid, while the correspondences 1), 2) and 1), 3) need not be mutually inverse. It is of interest, accordingly, to single out families of subrings and families of subgroups for which the analogue of the theorem on Galois correspondence is valid. This problem has found a positive solution in two cases. The first one involves the requirements of "proximity" between the properties of the ring 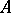 and the properties of a field (e.g.
and the properties of a field (e.g. 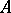 is a skew-field or a complete ring of linear transformations of a vector space over a skew-field); the second is the requirement of "proximity" between the structure of the ring
is a skew-field or a complete ring of linear transformations of a vector space over a skew-field); the second is the requirement of "proximity" between the structure of the ring 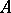 over a subring
over a subring 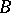 to the structure of the corresponding pair if
to the structure of the corresponding pair if 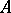 is a field (e.g. the
is a field (e.g. the 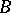 -module is projective).
-module is projective).
Let  be an invertible element of the ring
be an invertible element of the ring 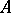 , let
, let 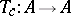 be the automorphism of
be the automorphism of  defined by
defined by 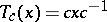 ,
, 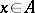 , and let
, and let 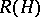 be the subalgebra of
be the subalgebra of  generated by the invertible elements
generated by the invertible elements  for which
for which 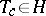 . The group
. The group 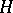 is called an
is called an 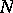 -group if
-group if  for all invertible
for all invertible 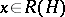 . If
. If  is a skew-field, if
is a skew-field, if 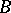 is a sub-skew-field of it, if
is a sub-skew-field of it, if  , and if
, and if  is a finite-dimensional left vector space over
is a finite-dimensional left vector space over 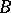 , then the Galois correspondences
, then the Galois correspondences 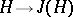 and
and 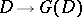 are mutually inverse, where
are mutually inverse, where 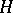 belongs to the set of all
belongs to the set of all 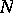 -subgroups of the group
-subgroups of the group 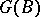 and
and 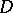 to the set of all skew-fields of the sub-skew-field
to the set of all skew-fields of the sub-skew-field 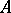 containing
containing 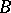 .
.
A similar result is also valid if  is a complete ring of linear transformations (but the corresponding system of conditions singling out the families of subgroups and families of subrings is formulated in a somewhat more complicated manner).
is a complete ring of linear transformations (but the corresponding system of conditions singling out the families of subgroups and families of subrings is formulated in a somewhat more complicated manner).
Further, let  be a commutative ring without non-trivial idempotents and let
be a commutative ring without non-trivial idempotents and let  . The ring
. The ring 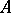 is called a finite normal extension of a ring
is called a finite normal extension of a ring  if
if 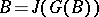 and
and 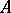 is a finitely-generated
is a finitely-generated 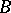 -module. The ring
-module. The ring 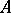 may be considered to be an
may be considered to be an 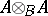 -module by assuming
-module by assuming
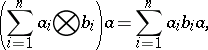 |
where 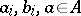 . The ring
. The ring 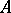 is called a separable
is called a separable 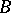 -algebra if
-algebra if 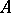 is a projective
is a projective  -module. If
-module. If  is a finite normal separable extension of the ring
is a finite normal separable extension of the ring 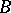 , then
, then  is a finitely-generated projective
is a finitely-generated projective  -module, the group
-module, the group 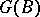 is finite
is finite 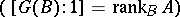 and the mappings
and the mappings 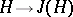 ,
, 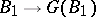 define mutually-inverse relations between the set of all subgroups of the group
define mutually-inverse relations between the set of all subgroups of the group 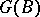 and the set of all separable
and the set of all separable 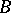 -subalgebras of the algebra
-subalgebras of the algebra 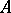 .
.
Any ring 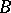 has a separable closure, which is an analogue of the separable closure of a field. The group of all automorphisms of this closure which leave
has a separable closure, which is an analogue of the separable closure of a field. The group of all automorphisms of this closure which leave 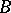 invariant elementwise is, in the general case, a profinite group. The correspondences 1) and 2) are mutually inverse on the set of all closed subgroups of the resulting group and on the set of all separable
invariant elementwise is, in the general case, a profinite group. The correspondences 1) and 2) are mutually inverse on the set of all closed subgroups of the resulting group and on the set of all separable 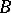 -subalgebras of the separable closure of the ring
-subalgebras of the separable closure of the ring 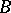 .
.
Similar results are also valid if the ring 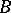 contains non-trivial idempotents. However, this involves substantial changes in a number of basic concepts. For instance, the role of the Galois group
contains non-trivial idempotents. However, this involves substantial changes in a number of basic concepts. For instance, the role of the Galois group  is taken over by the fundamental groupoid.
is taken over by the fundamental groupoid.
References
| [1] | N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956) MR0081264 Zbl 0073.02002 |
| [2] | S.U. Chase, M.E. Swedler, "Hopf algebras and Galois theory" , Springer (1969) MR0260724 Zbl 0197.01403 |
| [3] | F. de Meyer, E. Ingraham, "Separable algebras over commutative rings" , Lect. notes in math. , 181 , Springer (1971) MR280479 |
| [4] | A.R. Magid, "The separable Galois theory of commutative rings" , M. Dekker (1974) MR0352075 Zbl 0284.13004 |
Comments
References
| [a1] | S.U. Chase, D.K. Harrison, A. Rosenberg, "Galois theory and Galois cohomology of commutative rings" , Mem. Amer. Math. Soc. , 52 , Amer. Math. Soc. (1965) MR0195922 Zbl 0143.05902 |
Galois theory of rings. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Galois_theory_of_rings&oldid=24073