Galois theory of rings

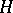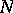A generalization of the results of the theory of Galois fields (cf. Galois theory and Galois group) to the case of associative rings with a unit element. Let be an associative ring with a unit element, let be some subgroup of the group of all automorphisms of , let be a subgroup of 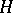, let

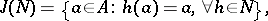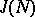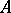and let . The set will then be a subring of . Let be a subring of . One says that an automorphism 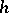of 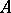leaves 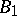invariant elementwise if 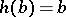for all 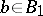. The set of all such automorphisms is denoted by 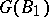. Let

The principal subject of the Galois theory of rings are the correspondences:

1) ;

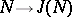2) ;

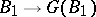3) 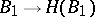. Unlike the Galois theory of fields, (even when the group 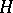is finite) the equality 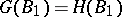is not always valid, while the correspondences 1), 2) and 1), 3) need not be mutually inverse. It is of interest, accordingly, to single out families of subrings and families of subgroups for which the analogue of the theorem on Galois correspondence is valid. This problem has found a positive solution in two cases. The first one involves the requirements of "proximity" between the properties of the ring 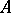and the properties of a field (e.g. 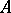is a skew-field or a complete ring of linear transformations of a vector space over a skew-field); the second is the requirement of "proximity" between the structure of the ring 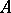over a subring 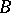to the structure of the corresponding pair if 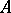is a field (e.g. the 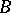-module is projective).

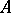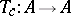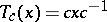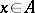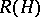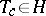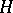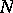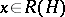Let be an invertible element of the ring , let be the automorphism of defined by , , and let be the subalgebra of generated by the invertible elements for which . The group is called an -group if for all invertible . If is a skew-field, if 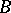is a sub-skew-field of it, if , and if is a finite-dimensional left vector space over 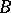, then the Galois correspondences 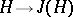and 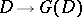are mutually inverse, where 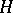belongs to the set of all 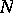-subgroups of the group 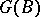and 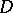to the set of all skew-fields of the sub-skew-field 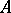containing .

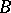A similar result is also valid if is a complete ring of linear transformations (but the corresponding system of conditions singling out the families of subgroups and families of subrings is formulated in a somewhat more complicated manner).

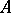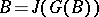Further, let be a commutative ring without non-trivial idempotents and let . The ring is called a finite normal extension of a ring if and 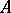is a finitely-generated 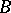-module. The ring 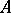may be considered to be an 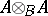-module by assuming

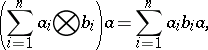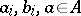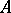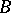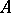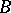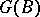where . The ring is called a separable -algebra if is a projective -module. If is a finite normal separable extension of the ring , then is a finitely-generated projective -module, the group is finite 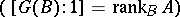and the mappings 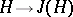, 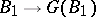define mutually-inverse relations between the set of all subgroups of the group 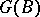and the set of all separable 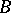-subalgebras of the algebra .

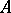Any ring 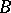has a separable closure, which is an analogue of the separable closure of a field. The group of all automorphisms of this closure which leave 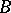invariant elementwise is, in the general case, a profinite group. The correspondences 1) and 2) are mutually inverse on the set of all closed subgroups of the resulting group and on the set of all separable 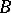-subalgebras of the separable closure of the ring .

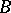Similar results are also valid if the ring 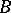contains non-trivial idempotents. However, this involves substantial changes in a number of basic concepts. For instance, the role of the Galois group is taken over by the fundamental groupoid.

References

[1]	N. Jacobson, "Structure of rings" , Amer. Math. Soc. (1956)
[2]	S.U. Chase, M.E. Swedler, "Hopf algebras and Galois theory" , Springer (1969)
[3]	F. de Meyer, E. Ingraham, "Separable algebras over commutative rings" , Lect. notes in math. , 181 , Springer (1971)
[4]	A.R. Magid, "The separable Galois theory of commutative rings" , M. Dekker (1974)

References

[a1]	S.U. Chase, D.K. Harrison, A. Rosenberg, "Galois theory and Galois cohomology of commutative rings" , Mem. Amer. Math. Soc. , 52 , Amer. Math. Soc. (1965)