Difference between revisions of "Veronese mapping"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 18: | Line 18: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) {{MR|0447223}} {{ZBL|0362.14001}} </TD></TR></table> |
| Line 26: | Line 26: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) pp. 178; 674; 179; 349; 525; 532; 535; 632; 743 {{MR|0507725}} {{ZBL|0408.14001}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 13; 170; 316; 381 {{MR|0463157}} {{ZBL|0367.14001}} </TD></TR></table> |
Revision as of 21:57, 30 March 2012
A special regular mapping of a projective space; named after G. Veronese. Let  be positive integers,
be positive integers, 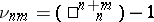 , and
, and 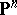 ,
, 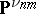 projective spaces over an arbitrary field (or over the ring of integers), regarded as schemes; let
projective spaces over an arbitrary field (or over the ring of integers), regarded as schemes; let  be projective coordinates in
be projective coordinates in 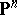 , and let
, and let 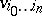 ,
, 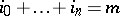 , be projective coordinates in
, be projective coordinates in 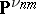 . The Veronese mapping is the morphism
. The Veronese mapping is the morphism
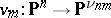 |
given by the formulas 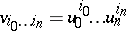 ,
, 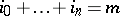 . The Veronese mapping may be defined in invariant terms as a regular mapping given by a complete linear system
. The Veronese mapping may be defined in invariant terms as a regular mapping given by a complete linear system  , where
, where 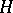 is a hyperplane section in
is a hyperplane section in 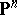 . The Veronese mapping is a closed imbedding; its image
. The Veronese mapping is a closed imbedding; its image 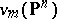 is called a Veronese variety, and is defined by the equations
is called a Veronese variety, and is defined by the equations
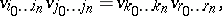 |
where  . For instance,
. For instance, 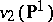 is the curve represented by the equation
is the curve represented by the equation 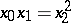 in
in 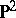 . The degree of a Veronese variety is
. The degree of a Veronese variety is 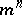 . For any hypersurface
. For any hypersurface
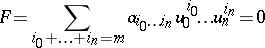 |
in  its image with respect to the Veronese mapping
its image with respect to the Veronese mapping 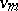 is the intersection of the Veronese variety
is the intersection of the Veronese variety 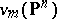 with the hyperplane
with the hyperplane
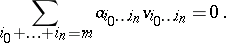 |
Owing to this fact, Veronese mappings may be used to reduce certain problems on hypersurfaces to the case of hyperplane sections.
References
| [1] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) MR0447223 Zbl 0362.14001 |
Comments
The image of 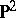 in
in 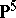 under the Veronese imbedding (
under the Veronese imbedding (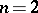 ,
, 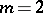 ) is called the Veronese surface.
) is called the Veronese surface.
References
| [a1] | P.A. Griffiths, J.E. Harris, "Principles of algebraic geometry" , Wiley (Interscience) (1978) pp. 178; 674; 179; 349; 525; 532; 535; 632; 743 MR0507725 Zbl 0408.14001 |
| [a2] | R. Hartshorne, "Algebraic geometry" , Springer (1977) pp. 13; 170; 316; 381 MR0463157 Zbl 0367.14001 |
Veronese mapping. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Veronese_mapping&oldid=24008