Difference between revisions of "Normal sheaf"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 30: | Line 30: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) {{MR|0447223}} {{ZBL|0362.14001}} </TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> R. Hartshorne, "Algebraic geometry" , Springer (1977) {{MR|0463157}} {{ZBL|0367.14001}} </TD></TR></table> |
Revision as of 21:54, 30 March 2012
An analogue to a normal bundle in sheaf theory. Let
 |
be a morphism of ringed spaces such that the homomorphism 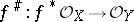 is surjective, and let
is surjective, and let 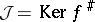 . Then
. Then 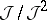 is a sheaf of ideals in
is a sheaf of ideals in 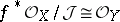 and is, therefore, an
and is, therefore, an 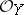 -module. Here
-module. Here 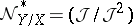 is called the conormal sheaf of the morphism and the dual
is called the conormal sheaf of the morphism and the dual 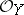 -module
-module 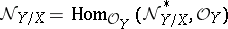 is called the normal sheaf of the morphism
is called the normal sheaf of the morphism  . These sheaves are, as a rule, examined in the following special cases.
. These sheaves are, as a rule, examined in the following special cases.
1) 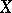 and
and 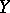 are differentiable manifolds (for example, of class
are differentiable manifolds (for example, of class 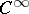 ), and
), and  is an immersion. There is an exact sequence of
is an immersion. There is an exact sequence of 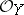 -modules
-modules
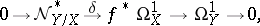 |
where 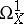 and
and 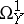 are the sheaves of germs of smooth
are the sheaves of germs of smooth 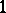 -forms on
-forms on 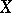 and
and 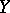 , and
, and 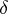 is defined as differentiation of functions. The dual exact sequence
is defined as differentiation of functions. The dual exact sequence
 |
where 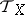 and
and 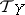 are the tangent sheaves on
are the tangent sheaves on 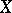 and
and 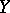 , shows that
, shows that 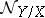 is isomorphic to the sheaf of germs of smooth sections of the normal bundle of the immersion
is isomorphic to the sheaf of germs of smooth sections of the normal bundle of the immersion 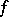 . If
. If 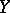 is an immersed submanifold, then
is an immersed submanifold, then 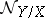 and
and 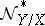 are called the normal and conormal sheaves of the submanifold
are called the normal and conormal sheaves of the submanifold 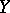 .
.
2) 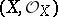 is an irreducible separable scheme of finite type over an algebraically closed field
is an irreducible separable scheme of finite type over an algebraically closed field 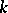 ,
, 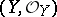 is a closed subscheme of it and
is a closed subscheme of it and 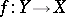 is an imbedding. Then
is an imbedding. Then 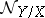 and
and 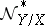 are called the normal and conormal sheaves of the subscheme
are called the normal and conormal sheaves of the subscheme 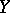 . There is also an exact sequence of
. There is also an exact sequence of 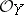 -modules
-modules
 | (*) |
where 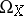 and
and 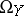 are the sheaves of differentials on
are the sheaves of differentials on 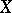 and
and 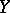 . The sheaves
. The sheaves 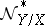 and
and 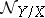 are quasi-coherent, and if
are quasi-coherent, and if 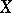 is a Noetherian scheme, then they are coherent. If
is a Noetherian scheme, then they are coherent. If 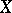 is a non-singular variety over
is a non-singular variety over 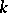 and
and 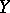 is a non-singular variety, then
is a non-singular variety, then 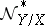 is locally free and the homomorphism
is locally free and the homomorphism 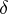 in (*) is injective. In this case one obtains the dual exact sequence
in (*) is injective. In this case one obtains the dual exact sequence
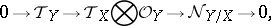 |
so that the normal sheaf 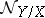 is locally free of rank
is locally free of rank 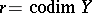 corresponding to the normal bundle over
corresponding to the normal bundle over 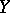 . In particular, if
. In particular, if 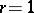 , then
, then 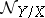 is the invertible sheaf corresponding to the divisor
is the invertible sheaf corresponding to the divisor 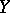 .
.
In terms of normal sheaves one can express the self-intersection 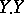 of a non-singular subvariety
of a non-singular subvariety 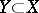 . Namely,
. Namely, 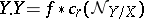 , where
, where 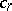 is the
is the  -th Chern class and
-th Chern class and 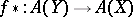 is the homomorphism of Chow rings (cf. Chow ring) corresponding to the imbedding
is the homomorphism of Chow rings (cf. Chow ring) corresponding to the imbedding 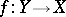 .
.
3) 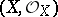 is a complex space,
is a complex space, 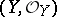 is a closed analytic subspace of it and
is a closed analytic subspace of it and 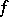 is the imbedding. Then
is the imbedding. Then  and
and 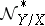 are called the normal and conormal sheaves of the subspace
are called the normal and conormal sheaves of the subspace 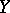 ; they are coherent. If
; they are coherent. If 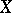 is an analytic manifold and
is an analytic manifold and 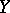 an analytic submanifold of it, then
an analytic submanifold of it, then 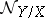 is the sheaf of germs of holomorphic sections of the normal bundle over
is the sheaf of germs of holomorphic sections of the normal bundle over 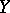 .
.
References
| [1] | I.R. Shafarevich, "Basic algebraic geometry" , Springer (1977) (Translated from Russian) MR0447223 Zbl 0362.14001 |
| [2] | R. Hartshorne, "Algebraic geometry" , Springer (1977) MR0463157 Zbl 0367.14001 |
Comments
If 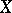 is a non-singular variety over
is a non-singular variety over 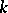 and
and 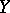 is a subscheme of
is a subscheme of 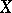 that is locally a complete intersection, then
that is locally a complete intersection, then 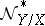 is locally free.
is locally free.
Normal sheaf. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Normal_sheaf&oldid=23917