Difference between revisions of "Mellin transform"
(Importing text file) |
Ulf Rehmann (talk | contribs) m (MR/ZBL numbers added) |
||
| Line 18: | Line 18: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[1]</TD> <TD valign="top"> H. Mellin, "Ueber die fundamentelle Wichtigkeit des Satzes von Cauchy für die Theorie der Gamma- und hypergeometrischen Funktionen" ''Acta Soc. Sci. Fennica'' , '''21''' : 1 (1896) pp. 1–115</TD></TR><TR><TD valign="top">[2]</TD> <TD valign="top"> H. Mellin, "Ueber den Zusammenhang zwischen linearen Differential- und Differenzengleichungen" ''Acta Math.'' , '''25''' (1902) pp. 139–164 {{MR|}} {{ZBL|32.0348.02}} </TD></TR><TR><TD valign="top">[3]</TD> <TD valign="top"> E.C. Titchmarsh, "Introduction to the theory of Fourier integrals" , Oxford Univ. Press (1948) {{MR|0942661}} {{ZBL|0017.40404}} {{ZBL|63.0367.05}} </TD></TR><TR><TD valign="top">[4]</TD> <TD valign="top"> V.A. Ditkin, A.P. Prudnikov, "Transformations intégrales et calcul opérationnel" , MIR (1978) (Translated from Russian) {{MR|0622209}} {{MR|0622210}} {{ZBL|0375.44001}} </TD></TR></table> |
| Line 32: | Line 32: | ||
====References==== | ====References==== | ||
| − | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> | + | <table><TR><TD valign="top">[a1]</TD> <TD valign="top"> E. Hecke, "Ueber die Bestimmung Dirichletscher Reihen durch ihre Funktionalgleichung" ''Math. Ann.'' , '''112''' (1936) pp. 664–699 {{MR|}} {{ZBL|0014.01601}} {{ZBL|62.1207.01}} {{ZBL|63.0264.03}} </TD></TR><TR><TD valign="top">[a2]</TD> <TD valign="top"> A. Weil, "Ueber die Bestimmung Dirichletscher Reihen durch ihre Funktionalgleichung" ''Math. Ann.'' , '''168''' (1967) pp. 149–156</TD></TR><TR><TD valign="top">[a3]</TD> <TD valign="top"> A. Weil, "Zeta functions and Mellin transforms" , ''Algebraic geometry (Bombay Coll., 1968)'' , Oxford Univ. Press & Tata Inst. (1968) pp. 409–426 {{MR|0262247}} {{ZBL|0193.49104}} </TD></TR><TR><TD valign="top">[a4]</TD> <TD valign="top"> A. Ogg, "Modular forms and Dirichlet series" , Benjamin (1969) {{MR|0256993}} {{MR|0234918}} {{ZBL|0191.38101}} </TD></TR><TR><TD valign="top">[a5]</TD> <TD valign="top"> G. Shimura, "Introduction to the arithmetic theory of automorphic functions" , Princeton Univ. Press & Iwanami-Shoten (1971) pp. §3.6, pp 89–94 {{MR|0314766}} {{ZBL|0221.10029}} </TD></TR></table> |
Revision as of 21:54, 30 March 2012
The integral transform
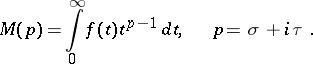 |
The substitution 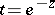 reduces it to the Laplace transform. The Mellin transform is used for solving a specific class of planar problems for harmonic functions in a sectorial domain, of problems in elasticity theory, etc.
reduces it to the Laplace transform. The Mellin transform is used for solving a specific class of planar problems for harmonic functions in a sectorial domain, of problems in elasticity theory, etc.
The inversion theorem. Suppose that 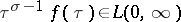 and that the function
and that the function 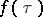 has bounded variation in a neighbourhood of the point
has bounded variation in a neighbourhood of the point 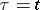 . Then
. Then
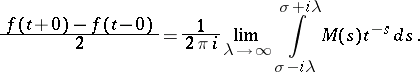 |
The representation theorem. Suppose that the function 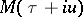 is summable with respect to
is summable with respect to  on
on 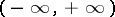 and has bounded variation in a neighbourhood of the point
and has bounded variation in a neighbourhood of the point  . Then
. Then
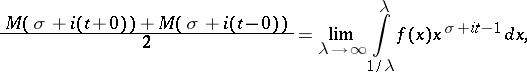 |
where
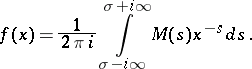 |
References
| [1] | H. Mellin, "Ueber die fundamentelle Wichtigkeit des Satzes von Cauchy für die Theorie der Gamma- und hypergeometrischen Funktionen" Acta Soc. Sci. Fennica , 21 : 1 (1896) pp. 1–115 |
| [2] | H. Mellin, "Ueber den Zusammenhang zwischen linearen Differential- und Differenzengleichungen" Acta Math. , 25 (1902) pp. 139–164 Zbl 32.0348.02 |
| [3] | E.C. Titchmarsh, "Introduction to the theory of Fourier integrals" , Oxford Univ. Press (1948) MR0942661 Zbl 0017.40404 Zbl 63.0367.05 |
| [4] | V.A. Ditkin, A.P. Prudnikov, "Transformations intégrales et calcul opérationnel" , MIR (1978) (Translated from Russian) MR0622209 MR0622210 Zbl 0375.44001 |
Comments
If 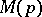 denotes the Mellin transform of
denotes the Mellin transform of 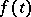 , then the Parseval equality takes the form:
, then the Parseval equality takes the form:
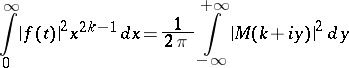 |
if 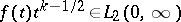 .
.
The Mellin transform also serves to link Dirichlet series with automorphic functions (cf. Automorphic function); in particular, the inversion formula plays a role in the proof of a functional equation for Dirichlet series similar to that for the Riemann zeta-function. Cf. [a1]–[a5].
References
| [a1] | E. Hecke, "Ueber die Bestimmung Dirichletscher Reihen durch ihre Funktionalgleichung" Math. Ann. , 112 (1936) pp. 664–699 Zbl 0014.01601 Zbl 62.1207.01 Zbl 63.0264.03 |
| [a2] | A. Weil, "Ueber die Bestimmung Dirichletscher Reihen durch ihre Funktionalgleichung" Math. Ann. , 168 (1967) pp. 149–156 |
| [a3] | A. Weil, "Zeta functions and Mellin transforms" , Algebraic geometry (Bombay Coll., 1968) , Oxford Univ. Press & Tata Inst. (1968) pp. 409–426 MR0262247 Zbl 0193.49104 |
| [a4] | A. Ogg, "Modular forms and Dirichlet series" , Benjamin (1969) MR0256993 MR0234918 Zbl 0191.38101 |
| [a5] | G. Shimura, "Introduction to the arithmetic theory of automorphic functions" , Princeton Univ. Press & Iwanami-Shoten (1971) pp. §3.6, pp 89–94 MR0314766 Zbl 0221.10029 |
Mellin transform. Encyclopedia of Mathematics. URL: http://encyclopediaofmath.org/index.php?title=Mellin_transform&oldid=23896